【题目】如图1,在△ABC中,∠BAC=90°,AB=AC,直线MN过点A,且MN∥BC,点D是直线MN上一点,不与点A重合.若点E是线段AB上一点,且DE=DA.
(1)请说明线段DE⊥DA.
(2)如图2,连接BD,过点D作DP⊥DB交线段AC于点P,请判断线段DB与DP的数量关系,并说明理由.

参考答案:
【答案】(1)见解析;(2)DB=DP,理由见解析.
【解析】
(1)根据等腰直角三角形的性质得到∠B=45°,根据平行线的性质、垂直的定义证明;
(3)利用ASA定理证明△BDF≌△PDA,根据全等三角形的性质证明即可;
解:(1)∵∠BAC=90°,AB=AC,
∴∠B=∠C=45°.
∵MN∥BC,
∴∠DAE=∠B=45°.
∵DA=DE,
∴∠DEA=∠DAE=45°,
∴∠ADE=180°-∠DEA-∠DAE=90°,
∴DE⊥DA.
(2)DB=DP.
理由如下:∵DP⊥DB,
∴∠BDE+∠EDP=90°.
由(1)知DE⊥DA,
∴∠ADP+∠EDP=90°,
∴∠BDE=∠ADP.
∵∠DEA=∠DAE=45°,
∴∠BED=180°-45°=135°,∠DAP=∠DAE+∠BAC=135°,
∴∠BED=∠DAP.
在△DEB和△DAP中,
 ,
,
∴△DEB≌△DAP(ASA),
∴DB=DP.
-
科目: 来源: 题型:
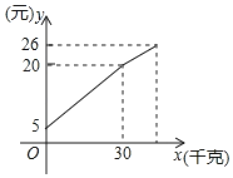
查看答案和解析>>【题目】一农民带了若干千克土豆进城出售,为了方便,他带了一些零用钱备用,按市场价出售一些土豆后,又降价出售,售出土豆的千克数与他手中持有的钱数(含备用钱)的关系如图.结合图象回答:
(1)农民自带的零钱是 元;
(2)降价前他每千克土豆出售的价格是 元/千克;列出降价前售出土豆的千克数与他手中持有的钱数(含备用钱)的函数关系式为: ;
(3)降价后他按每千克0.4元将土豆售完,这时他手中的钱(含备用钱)是26元,问他一共带了多少土豆去城里出售?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图山坡上有一根旗杆AB,旗杆底部B点到山脚C点的距离BC为
 米,斜坡BC的坡度i=1:
米,斜坡BC的坡度i=1:  .小明在山脚的平地F处测量旗杆的高,点C到测角仪EF的水平距离CF=1米,从E处测得旗杆顶部A的仰角为45°,旗杆底部B的仰角为20°.
.小明在山脚的平地F处测量旗杆的高,点C到测角仪EF的水平距离CF=1米,从E处测得旗杆顶部A的仰角为45°,旗杆底部B的仰角为20°.(1)求坡角∠BCD;
(2)求旗杆AB的高度.
(参考数值:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)

-
科目: 来源: 题型:
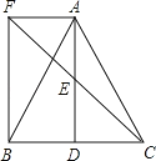
查看答案和解析>>【题目】如图,△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
(1)求证:△AEF≌△DEC;
(2)若AB=AC,试判断四边形AFBD的形状,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数形结合是解决数学问题的一种重要的思想方法,借助图的直观性,可以帮助理解数学问题.
(1)请写出图1、图2、图3分别能解释的乘法公式.


(2)用4个全等的长和宽分别为
 、
、 的长方形拼摆成一个如图4的正方形,请你写出这三个代数式
的长方形拼摆成一个如图4的正方形,请你写出这三个代数式 、
、 、
、 之间的等量关系.
之间的等量关系.(3)根据(2)中你探索发现的结论,完成下列问题:
①当
 ,
, 时, 则
时, 则 的值为 .
的值为 .②设
 ,
, ,计算:
,计算: 的结果.
的结果. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b的图象与反比例函数y=
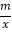 的图象相交于A、B两点.利用图中条件
的图象相交于A、B两点.利用图中条件(1)求反比例函数与一次函数的关系式;
(2)根据图象写出使该一次函数的值大于该反比例函数的值的x的取值范围;
(3)求出△AOB的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长方形ABCD中, AB=8cm,BC=12cm,点P从点B出发,以2cm/秒的速度沿BC向点C运动,设点P的运动时间为t秒.
(1)如图1,S△DCP = .(用t的代数式表示)
(2)如图1,当t=3时,试说明:△ABP≌△DCP.
(3)如图2,当点P从点B开始运动的同时,点Q从点C出发,以v cm/秒的速度沿CD向点D运动,是否存在这样v的值,使得△ABP与△PQC全等?若存在,请求出v的值;若不存在,请说明理由.

相关试题

