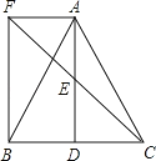
【题目】如图,△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
(1)求证:△AEF≌△DEC;
(2)若AB=AC,试判断四边形AFBD的形状,并证明你的结论.
参考答案:
【答案】(1)详见解析;(2):若AB=AC,则四边形AFBD是矩形,理由详见解析.
【解析】
(1)根据两直线平行,内错角相等求出∠AFE=∠DCE,∠FAE=∠CDE,然后利用“角角边”证明△AEF和△DEC全等;
(2)由(1)知AF平行等于BD,易证四边形AFBD是平行四边形,而AB=AC,AD是中线,利用等腰三角形三线合一定理,可证AD⊥BC,即∠ADB=90°,那么可证四边形AFBD是矩形.
(1)证明:∵AF∥BC,
∴∠AFE=∠DCE,∠FAE=∠CDE,
∵点E为AD的中点,
∴AE=DE,
在△AEF和△DEC中,
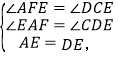
∴△AEF≌△DEC(AAS);
(2)解:若AB=AC,则四边形AFBD是矩形.理由如下:
∵AF∥BD,AF=BD,
∴四边形AFBD是平行四边形,
∵△AEF≌△DEC,
∴AF=CD,
∵AF=BD,
∴CD=BD;
∵AB=AC,BD=CD,
∴∠ADB=90°,
∴平行四边形AFBD是矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某运动品牌专卖店准备购进甲、乙两种运动鞋.其中甲、乙两种运动鞋的进价和售价如下表.已知购进60双甲种运动鞋与50双乙种运动鞋共用10000元
运动鞋价格
甲
乙
进价(元/双)
m
m﹣20
售价(元/双)
240
160
(1)求m的值;
(2)要使购进的甲、乙两种运动鞋共200双的总利润(利润=售价﹣进价)超过21000元,且不超过22000元,问该专卖店有几种进货方案?
(3)在(2)的条件下,专卖店准备决定对甲种运动鞋每双优惠a(50<a<70)元出售,乙种运动鞋价格不变.那么该专卖店要获得最大利润应如何进货?
-
科目: 来源: 题型:
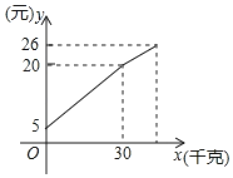
查看答案和解析>>【题目】一农民带了若干千克土豆进城出售,为了方便,他带了一些零用钱备用,按市场价出售一些土豆后,又降价出售,售出土豆的千克数与他手中持有的钱数(含备用钱)的关系如图.结合图象回答:
(1)农民自带的零钱是 元;
(2)降价前他每千克土豆出售的价格是 元/千克;列出降价前售出土豆的千克数与他手中持有的钱数(含备用钱)的函数关系式为: ;
(3)降价后他按每千克0.4元将土豆售完,这时他手中的钱(含备用钱)是26元,问他一共带了多少土豆去城里出售?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图山坡上有一根旗杆AB,旗杆底部B点到山脚C点的距离BC为
 米,斜坡BC的坡度i=1:
米,斜坡BC的坡度i=1:  .小明在山脚的平地F处测量旗杆的高,点C到测角仪EF的水平距离CF=1米,从E处测得旗杆顶部A的仰角为45°,旗杆底部B的仰角为20°.
.小明在山脚的平地F处测量旗杆的高,点C到测角仪EF的水平距离CF=1米,从E处测得旗杆顶部A的仰角为45°,旗杆底部B的仰角为20°.(1)求坡角∠BCD;
(2)求旗杆AB的高度.
(参考数值:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在△ABC中,∠BAC=90°,AB=AC,直线MN过点A,且MN∥BC,点D是直线MN上一点,不与点A重合.若点E是线段AB上一点,且DE=DA.
(1)请说明线段DE⊥DA.
(2)如图2,连接BD,过点D作DP⊥DB交线段AC于点P,请判断线段DB与DP的数量关系,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】数形结合是解决数学问题的一种重要的思想方法,借助图的直观性,可以帮助理解数学问题.
(1)请写出图1、图2、图3分别能解释的乘法公式.


(2)用4个全等的长和宽分别为
 、
、 的长方形拼摆成一个如图4的正方形,请你写出这三个代数式
的长方形拼摆成一个如图4的正方形,请你写出这三个代数式 、
、 、
、 之间的等量关系.
之间的等量关系.(3)根据(2)中你探索发现的结论,完成下列问题:
①当
 ,
, 时, 则
时, 则 的值为 .
的值为 .②设
 ,
, ,计算:
,计算: 的结果.
的结果. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b的图象与反比例函数y=
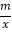 的图象相交于A、B两点.利用图中条件
的图象相交于A、B两点.利用图中条件(1)求反比例函数与一次函数的关系式;
(2)根据图象写出使该一次函数的值大于该反比例函数的值的x的取值范围;
(3)求出△AOB的面积.

相关试题

