【题目】如图,在平行四边形![]() 中,
中,![]() 为
为![]() 边上的点,
边上的点,![]() ,将
,将![]() 沿
沿![]() 翻折,点
翻折,点![]() 的对应点
的对应点![]() 恰好落在
恰好落在![]() 上,
上,![]() ,则
,则![]() ________.
________.

参考答案:
【答案】32°.
【解析】
由折叠的性质:∠DFE=∠A,设∠BEC=x,由等腰三角形的性质得出∠BCE=∠BEC=x,与平行四边形的性质得出∠A=∠BCD,AB∥CD,得出∠DCF=∠BEC=x,∠DFE=∠A=∠BCD=2x,在四边形ADFE中,由四边形内角和定理得出方程,解方程即可.
解:由折叠的性质可得:∠DFE=∠A,
设∠BEC=x,
∵BE=BC,
∴∠BCE=∠BEC=x,
∵四边形ABCD是平行四边形,
∴∠A=∠BCD,AB∥CD,
∴∠DCF=∠BEC=x,
∴∠DFE=∠A=∠BCD=2x,
在四边形ADFE中,∠A+∠ADF+∠DFE+∠AEF=360°,
∴2x+84°+2x+180°-x=360°,
解得:x=32°,
∴∠BEC=32°;
故答案为:32°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把菱形
 沿
沿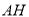 折叠,
折叠, 落在
落在 边上的
边上的 处,若
处,若 ,则
,则 的大小为( )
的大小为( )
A.
 B.
B. C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场为了吸引顾客,设立了一个可以自由转动的转盘(如下图),并规定:购买100元的商品,就能获得一次转动转盘的机会,如果转盘停止后,指针正好对准红、绿、黄、白区域,那么顾客就可以分别得到80元、30元、10元、0元的购物券,凭购物券仍然可以在商场购物;如果顾客不愿意转转盘,那么可以直接获得购物券10元.
(1)每转动一次转盘所获购物券金额的平均数是多少?
(2)若在此商场购买100元的货物,那么你将选择哪种方式获得购物券?
(3)小明在家里也做了一个同样的转盘做实验,转10次后共获得购物券96元,他说还是不转转盘直接领取购物券合算,你同意小明的说法吗?请说明理由.
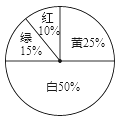
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2+3x+1﹣m=0有两个不相等的实数根.
(1)求m的取值范围;
(2)若m为负整数,求此时方程的根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校想了解学生每周的课外阅读时间情况,随机调查了部分学生,对学生每周的课外阅读时间x(单位:小时)进行分组整理,并绘制了如图所示的不完整的频数分布直方图和扇形统计图:

根据图中提供的信息,解答下列问题:
(1)共随机调查了___名学生,课外阅读时间在68小时之间有___人,并补全频数分布直方图;
(2)求扇形统计图中m的值和E组对应的圆心角度数;
(3)请估计该校3000名学生每周的课外阅读时间不小于6小时的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某旅行社组织一批游客外出旅游,原计划租用30座客车若干辆,但有15人没有座位;若租用同样数量的45座客车,则多出一辆车,且其余客车恰好坐满。已知30座客车租金为每辆220元,45座客车租金为每辆300元,问:
(1)这批游客的总人数是多少?原计划租用多少辆30座客车?
(2)若租用同一种客车,要使每位游客都有座位,应该怎样租用才合算?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:⊙O为Rt△ABC的外接圆,点D在边AC上,AD=AO;
(1)如图1,若弦BE∥OD,求证:OD=BE;
(2)如图2,点F在边BC上,BF=BO,若OD=2
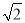 , OF=3,求⊙O的直径.
, OF=3,求⊙O的直径.
相关试题

