Question

【题目】已知：⊙O为Rt△ABC的外接圆，点D在边AC上，AD=AO；

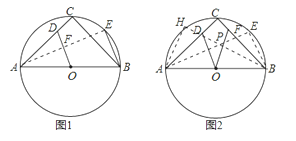
（1）如图1，若弦BE∥OD，求证：OD=BE；

（2）如图2，点F在边BC上，BF=BO，若OD=2 ， OF=3，求⊙O的直径．

Answer 1

【答案】（1）证明见解析；（2）圆的直径为．

【解析】试题分析：（1）连接AE交OD于点F，由AB为直径，利用直角所对的圆周角为直角得到AE与BE垂直，再由BE与OD平行，得到AE垂直于OD，再由AD=AO，利用三线合一得到AE为角平分线，且F为OD中点，利用中位线定理得到BE=2OF，等量代换即可得证；

（2）分别作弦BE∥OD，AH∥OF，连接AE，BH，AE与BH交于点P，由（1）得到E与H分别为弧BC与弧AC的中点，进而确定出∠HAE=∠HBE=45°，根据AB为直径，得到所对的圆周角为直角，确定出三角形APH与三角形BEP都为等腰直角三角形，由AP+PE求出AE的长，在直角三角形AEB中，利用勾股定理求出AB的长，即为圆的直径．

试题解析：解：（1）证明：连接AE交OD于点F．∵AB为直径，∴AE⊥BE，∵BE∥OD，∴AE⊥OD，∵AD=AO，∴AE平分∠CAB，∴OD=2OF，∵BE=2OF，∴BE=OD；

（2）分别作弦BE∥OD，AH∥OF，连接AE，BH，AE与BH交于点P，由（1）得：E为弧BC的中点，同理H为弧AC的中点，∴∠HAE=∠HBE=45°，∵AB为直径，∴∠H=∠E=90°，∴AP=AH，PE=BE，∵点O为AB的中点，BE∥OD，∴EB=OD=，∴PE=BE=，同理AH=OF=3，∴AP=，在Rt△ABE中，AE=，BE=，根据勾股定理得：AB=，则圆的直径为．