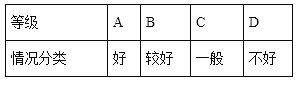
【题目】某校为了解本校七年级学生的数学作业完成情况,将完成情况分为四个等级:
随机对该年级若干名学生进行了调查,然后把调查结果绘制成两幅不完整的统计图.请根据图中的信息解答下列问题:
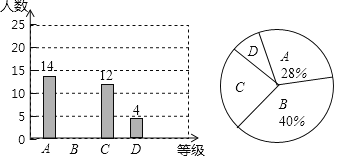
(1)共调查了多少名同学?补全条形统计图;
(2)完成等级为C等的对应扇形的圆心角的度数是 ;
(3)该年级共有700人,估计该年级数学作业完成等级为D等的人数.
参考答案:
【答案】(1)50名同学,见解析;(2)86.4°;(3)56人.
【解析】
(1)根据A等学生人数除以它所占的百分比求得共调查的人数,然后乘以B等所占的百分比求得B等人数,从而补全条形图;
(2)用360°乘以数学作业完成等级为C等的人数所占百分比即可求解;
(3)用该年级学生总数乘以数学作业完成等级为D等的人数所占百分比即可求解.
解:(1)总人数为14÷28%=50(人),
B等人数为50×40%=20(人).
条形图补充如下:

答:共调查了50名同学;
(2)完成等级为C等的对应扇形的圆心角的度数是:
360°×![]() =86.4°;
=86.4°;
故答案为:86.4°;
(3)该年级数学作业完成等级为D等的人数为700×![]() =56(人).
=56(人).
答:估计该年级数学作业完成等级为D等的人数是56人.
-
科目: 来源: 题型:
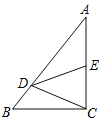
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,点D在边AB上,线段DC绕点D逆时针旋转,端点C恰巧落在边AC上的点E处.如果
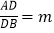 ,
,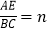
求m与n满足的关系式(用含n的代数式表示m).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠1+∠2=180°,∠B=∠3,∠BCD=80°,求∠ADC的度数.

解:∵∠1+∠2=180°,(已知)
∴ ∥ .( )
∴∠B=∠DEC.( )
∵∠B=∠3,(已知)
∴
∴AD∥BC,( )
∴ (两直线平行,同旁内角互补)
∵∠BCD=80°,
∴∠ADC= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果三角形有一边上的中线长恰好等于这条边的长,那么称这个三角形为“有趣三角形”,这条中线称为“有趣中线”.已知
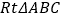 中,
中,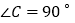 ,一条直角边为3,如果
,一条直角边为3,如果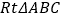 是“有趣三角形”,那么这个三角形“有趣中线”的长等于________.
是“有趣三角形”,那么这个三角形“有趣中线”的长等于________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=3x+3与x轴交于点A,与y轴交于点B.过B点作直线BP与x轴正半轴交于点P,取线段OA、OB、OP,当其中一条线段的长是其他两条线段长度的比例中项时,求P点的坐标
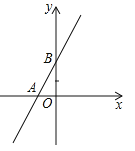
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形
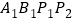 的顶点
的顶点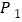 、
、 在反比例函数
在反比例函数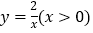 的图象上,顶点
的图象上,顶点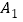 、
、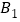 分别在
分别在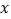 轴、
轴、 轴的正半轴上,再在其右侧作正方形
轴的正半轴上,再在其右侧作正方形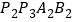 ,顶点
,顶点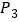 在反比例函数
在反比例函数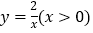 的图象上,顶点
的图象上,顶点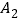 在
在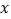 轴的正半轴上,则点
轴的正半轴上,则点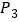 的坐标为____.
的坐标为____.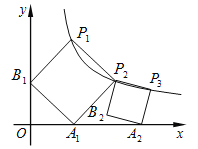
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某市郊外景区内一条笔直的公路a经过三个景点A、B、C,景区管委会又开发了风景优美的景点D,经测量景点D位于景点A的北偏东30°方向8km处,位于景点B的正北方向,还位于景点C的北偏西75°方向上,已知AB=5km.

(1)景区管委会准备由景点D向公路a修建一条距离最短的公路,不考虑其它因素,求出这条公路的长;(结果精确到0.1km)
(2)求景点C与景点D之间的距离.(结果精确到1km)
(参考数据:
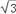 =1.73,
=1.73, =2.24,sin53°=cos37°=0.80,sin37°=cos53°=0.60,tan53°=1.33,tan37°=0.75,sin38°=cos52°=0.62,sin52°=cos38°=0.79,tan38°=0.78,tan52°=1.28,sin75°=0.97,cos75°=0.26,tan75°=3.73.)
=2.24,sin53°=cos37°=0.80,sin37°=cos53°=0.60,tan53°=1.33,tan37°=0.75,sin38°=cos52°=0.62,sin52°=cos38°=0.79,tan38°=0.78,tan52°=1.28,sin75°=0.97,cos75°=0.26,tan75°=3.73.)
相关试题

