【题目】如果三角形有一边上的中线长恰好等于这条边的长,那么称这个三角形为“有趣三角形”,这条中线称为“有趣中线”.已知![]() 中,
中,![]() ,一条直角边为3,如果
,一条直角边为3,如果![]() 是“有趣三角形”,那么这个三角形“有趣中线”的长等于________.
是“有趣三角形”,那么这个三角形“有趣中线”的长等于________.
参考答案:
【答案】![]() 或3.
或3.
【解析】
“有趣中线”分别三种情况,两个直角边跟斜边,而直角三角形的斜边的中点到三顶点距离相等,不符合;两个直角边,有一种情况有趣中线为3.或另一条直角边为3,利用勾股定理求出即可.
“有趣中线”有三种情况:
若“有趣中线”为斜边AB上的中线,直角三角形的斜边的中线等于斜边的一半,不合题意;
若“有趣中线”BD=AC=3;
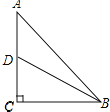
若“有趣中线”为BD,如图所示,

BC=3,
设BD=2x,则CD=x,
在Rt△CBD中,根据勾股定理得:BD2=BC2+CD2,即(2x)2=32+x2,
解得:x=![]() ,
,
则△ABC的“有趣中线”的长等于![]() 或3.
或3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,∠A=70°,将平行四边形ABCD绕点B顺时针旋转到平行四边形A1BC1D1的位置,此时C1D1恰好经过点C,则∠ABA1=______°.

-
科目: 来源: 题型:
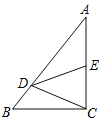
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,点D在边AB上,线段DC绕点D逆时针旋转,端点C恰巧落在边AC上的点E处.如果
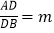 ,
,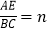
求m与n满足的关系式(用含n的代数式表示m).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠1+∠2=180°,∠B=∠3,∠BCD=80°,求∠ADC的度数.

解:∵∠1+∠2=180°,(已知)
∴ ∥ .( )
∴∠B=∠DEC.( )
∵∠B=∠3,(已知)
∴
∴AD∥BC,( )
∴ (两直线平行,同旁内角互补)
∵∠BCD=80°,
∴∠ADC= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了解本校七年级学生的数学作业完成情况,将完成情况分为四个等级:
随机对该年级若干名学生进行了调查,然后把调查结果绘制成两幅不完整的统计图.请根据图中的信息解答下列问题:
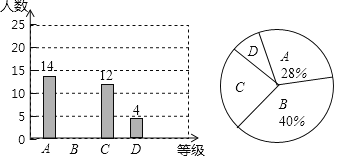
(1)共调查了多少名同学?补全条形统计图;
(2)完成等级为C等的对应扇形的圆心角的度数是 ;
(3)该年级共有700人,估计该年级数学作业完成等级为D等的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=3x+3与x轴交于点A,与y轴交于点B.过B点作直线BP与x轴正半轴交于点P,取线段OA、OB、OP,当其中一条线段的长是其他两条线段长度的比例中项时,求P点的坐标
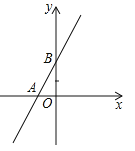
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形
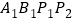 的顶点
的顶点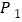 、
、 在反比例函数
在反比例函数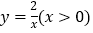 的图象上,顶点
的图象上,顶点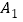 、
、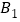 分别在
分别在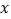 轴、
轴、 轴的正半轴上,再在其右侧作正方形
轴的正半轴上,再在其右侧作正方形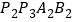 ,顶点
,顶点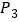 在反比例函数
在反比例函数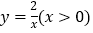 的图象上,顶点
的图象上,顶点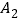 在
在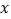 轴的正半轴上,则点
轴的正半轴上,则点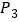 的坐标为____.
的坐标为____.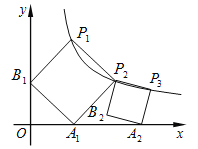
相关试题

