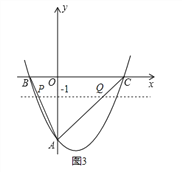
【题目】如图,经过点A(0,﹣4)的抛物线y=![]() x2+bx+c与x轴相交于B(﹣2,0),C两点,O为坐标原点;
x2+bx+c与x轴相交于B(﹣2,0),C两点,O为坐标原点;
(1)求抛物线的解析式并用配方法求顶点M的坐标;
(2)若抛物线上有一点P,使∠PCB=∠ABC,求P点坐标;
(3)将抛物线y=![]() x2+bx+c向上平移
x2+bx+c向上平移![]() 个单位长度,再向左平移m(m>0)个单位长度得到新抛物线,若新抛物线的顶点M在△ABC内,直接写出m的取值范围.
个单位长度,再向左平移m(m>0)个单位长度得到新抛物线,若新抛物线的顶点M在△ABC内,直接写出m的取值范围.

参考答案:
【答案】(1)y=![]() x2﹣x﹣4,(1,﹣
x2﹣x﹣4,(1,﹣![]() );(2)(2,﹣4)或(﹣6,20);(3)0<m<
);(2)(2,﹣4)或(﹣6,20);(3)0<m<![]() 。
。
【解析】试题分析:(1)只需运用待定系数法就可求出抛物线的解析式,然后用配方法就可求出顶点M的坐标;
(2)可分点P在x轴的下方和上方两种情况讨论,当点P在x轴下方时,根据抛物线的轴对称性得到点P的坐标;当点P在x轴上方时,直线PC与直线AB平行,可用待定系数法求出直线AB的解析式,然后再根据两平行直线一次项的系数相同,求出直线PC的解析式,然后只需求出直线PC与抛物线的交点坐标,就可解决问题;
(3)根据条件可得新抛物线的顶点M坐标为(1﹣m,﹣1),故点M始终在直线y=﹣1上.设直线y=﹣1与直线AB交于点P,与直线AC交于点Q,由点M在△ABC内可得点M在线段PQ上(不包括端点P、Q),只需求出点P、Q的坐标,就可解决问题.
试题解析:解:(1)∵点A(0,﹣4)、B(﹣2,0)在抛物线y=![]() x2+bx+c上,∴
x2+bx+c上,∴![]() ,解得:
,解得: ![]() ,∴抛物线的解析式为y=
,∴抛物线的解析式为y=![]() x2﹣x﹣4.
x2﹣x﹣4.
∵y=![]() x2﹣x﹣4=
x2﹣x﹣4=![]() (x2﹣2x+1﹣1)﹣4=
(x2﹣2x+1﹣1)﹣4=![]() (x﹣1)2﹣
(x﹣1)2﹣![]() ,∴抛物线的顶点M的坐标为(1,﹣
,∴抛物线的顶点M的坐标为(1,﹣![]() );
);
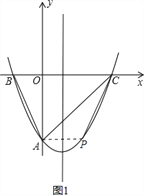
(2)①点P在x轴的下方,如图1,
∵∠PCB=∠ABC,点B与点C关于对称轴x=1对称,∴点A(0,﹣4)与点P也关于对称轴x=1对称,∴点P的坐标为(2,﹣4);
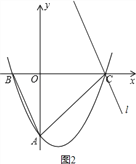
②点P在x轴的上方,直线PC记为直线l,如图2,
令y=0,得![]() (x﹣1)2﹣
(x﹣1)2﹣![]() =0,解得:x1=﹣2,x2=4,∴点C的坐标为(4,0).
=0,解得:x1=﹣2,x2=4,∴点C的坐标为(4,0).
设直线AB的解析式为y=kx+t,则有![]() ,解得:
,解得: ![]() ,∴直线AB的解析式为y=﹣2x﹣4.
,∴直线AB的解析式为y=﹣2x﹣4.
∵∠PCB=∠ABC,∴直线AB∥直线l,∴直线l可设为y=﹣2x+n.∵点C(4,0)在直线y=﹣2x+n上,∴﹣8+n=0,∴n=8,∴直线l的解析式为y=﹣2x+8,解方程组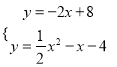 ,得
,得![]() 或
或![]() ,∴点P的坐标为(﹣6,20).
,∴点P的坐标为(﹣6,20).
综上所述:点P的坐标为(2,﹣4)或(﹣6,20);
(3)m的取值范围为0<m<![]() .
.
解题过程如下:
由题可得新抛物线顶点M的坐标为(1﹣m,﹣![]() +
+![]() )即(1﹣m,﹣1).
)即(1﹣m,﹣1).
设直线AC的解析式为y=px+q,则有![]() ,解得:
,解得: ![]() ,∴直线AC的解析式为y=x﹣4.
,∴直线AC的解析式为y=x﹣4.
设直线y=﹣1与直线AB交于点P,与直线AC交于点Q,如图3,
由﹣2x﹣4=﹣1,得:x=﹣![]() ,则点P的坐标为(﹣
,则点P的坐标为(﹣![]() ,﹣1);
,﹣1);
由x﹣4=﹣1,得:x=3,则点P的坐标为(3,﹣1).
∵新抛物线的顶点M(1﹣m,﹣1)在△ABC内,∴点M在线段PQ上(不包括端点P、Q),∴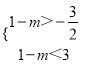 ,解得:﹣2<m<
,解得:﹣2<m<![]() .
.
∵m>0,∴m的取值范围为0<<m<![]() .
.
-
科目: 来源: 题型:
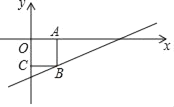
查看答案和解析>>【题目】如图所示,在第四象限内的矩形OABC,两边在坐标轴上,一个顶点在一次函数y=0.5x﹣3的图象上,当点A从左向右移动时,矩形的周长与面积也随之发生变化,设线段OA的长为m,矩形的周长为C,面积为S.
(1)试分别写出C、S与m的函数解析式,它们是否为一次函数?
(2)能否求出当m取何值时,矩形的周长最大?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】平衡车越来越受到中学生的喜爱,某公司今年从厂家以3000元/辆的批发价购进某品牌平衡车300辆进行销售,零售价格为4200元/辆,暑期将至,公司决定拿出一部分该品牌平衡车以4000元/辆的价格进行促销.设全部售出获得的总利润为y元,今年暑假期间拿出促销的该品牌平衡车数量为x辆,根据上述信息,解答下列问题:
(1)求y与x之间的函数解析式(也称关系式),并直接写出x的取值范围;
(2)若以促销价进行销售的数量不低于零售价销售数量的
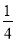 ,该公司应拿出多少辆该品牌平衡车促销才能使这批车的销售利润最大?并求出最大利润.
,该公司应拿出多少辆该品牌平衡车促销才能使这批车的销售利润最大?并求出最大利润. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,AB=12,AD=18,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,BG=
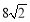 ,则△CEF的周长是 .
,则△CEF的周长是 .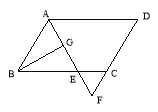
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲,乙两人同时各接受了600个零件的加工任务,甲比乙每分钟加工的数量多,两人同时开始加工,加工过程中其中一人因故障停止加工几分钟后又继续按原速加工,直到他们完成任务,如图表示甲比乙多加工的零件数量
 (个)与加工时间
(个)与加工时间 (分)之间的函数关系,观察图象解决下列问题:
(分)之间的函数关系,观察图象解决下列问题:(1)点B的坐标是________,B点表示的实际意义是___________ _____;
(2)求线段BC对应的函数关系式和D点坐标;
(3)乙在加工的过程中,多少分钟时比甲少加工100个零件?
(4)为了使乙能与甲同时完成任务,现让丙帮乙加工,直到完成.丙每分钟能加工3个零件,并把丙加工的零件数记在乙的名下,问丙应在第多少分钟时开始帮助乙?并在图中用虚线画出丙帮助后y与x之间的函数关系的图象.

-
科目: 来源: 题型:
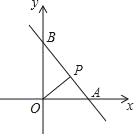
查看答案和解析>>【题目】如图,直线y=3﹣2x与x轴,y轴分别相交于点A,B,点P(x,y)是线段AB上的任意一点,并设△OAP的面积为S.
(1)S与x的函数解析式,求自变量x的取值范围.
(2)如果△OAP的面积大于1,求自变量x的取值范围.
-
科目: 来源: 题型:
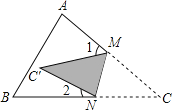
查看答案和解析>>【题目】如图,把△ABC纸片沿MN折叠,使点C落在四边形ABNM的内部时,则∠1、∠2和 ∠C之间有一种数量关系始终保持不变. 这个关系是___.
相关试题

