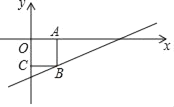
【题目】如图所示,在第四象限内的矩形OABC,两边在坐标轴上,一个顶点在一次函数y=0.5x﹣3的图象上,当点A从左向右移动时,矩形的周长与面积也随之发生变化,设线段OA的长为m,矩形的周长为C,面积为S.
(1)试分别写出C、S与m的函数解析式,它们是否为一次函数?
(2)能否求出当m取何值时,矩形的周长最大?为什么?
参考答案:
【答案】(1)C=m+6,面积S=﹣0.5m2+3m, C是m的一次函数,S不是m的一次函数;(2)不能求出当m取何值时,矩形的周长最大.
【解析】
(1)由题意可知A(m,0),B(m,0.5m﹣3),从而得AB=3﹣0.5m,继而根据矩形的周长公式和面积公式进行求解可得相应的函数解析式,然后再根据一次函数的概念进行判断即可;
(2)先确定出m的取值范围为0<m<6,根据(1)中的周长,可知m越大周长越大,但m没有是大值,因此不能求出当m取何值时,矩形的周长最大.
(1)由题意,可知A(m,0),B(m,0.5m﹣3),
则AB=|0.5m﹣3|=3﹣0.5m,
∴矩形的周长C=2(OA+AB)=2(m+3﹣0.5m)=m+6,
面积S=OAAB=m(3﹣0.5m)=﹣0.5m2+3m,
∴C是m的一次函数,S不是m的一次函数;
(2)不能求出当m取何值时,矩形的周长最大.
∵矩形OABC在第四象限内,
∴![]() ,
,
∴0<m<6,
又C=m+6,
∴不能求出当m取何值时,矩形的周长最大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】以正方形ABCD一边AB为边作等边三角形ABE,则∠CED=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将矩形ABCD绕点B顺时针旋转得到矩形A1BC1D1,点A、C、D的对应点分别为A1、C1、D1
(1)当点A1落在AC上时
①如图1,若∠CAB=60°,求证:四边形ABD1C为平行四边形;
②如图2,AD1交CB于点O.若∠CAB≠60°,求证:DO=AO;
(2)如图3,当A1D1过点C时.若BC=5,CD=3,直接写出A1A的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某校九年级男生在体能测试的引体向上项目的情况,随机抽取了部分男生引体向上项目的测试成绩,绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
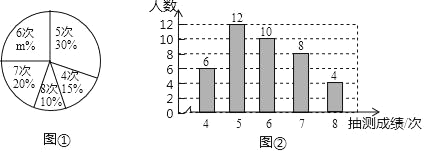
(Ⅰ)本次接受随机抽样调查的男生人数为 ,图①中m的值为 ;
(Ⅱ)求本次调查获取的样本数据的平均数、众数和中位数;
(Ⅲ)若规定引体向上6次及以上(含6次)为该项目良好,根据样本数据,估计该校320名九年级男生中该项目良好的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平衡车越来越受到中学生的喜爱,某公司今年从厂家以3000元/辆的批发价购进某品牌平衡车300辆进行销售,零售价格为4200元/辆,暑期将至,公司决定拿出一部分该品牌平衡车以4000元/辆的价格进行促销.设全部售出获得的总利润为y元,今年暑假期间拿出促销的该品牌平衡车数量为x辆,根据上述信息,解答下列问题:
(1)求y与x之间的函数解析式(也称关系式),并直接写出x的取值范围;
(2)若以促销价进行销售的数量不低于零售价销售数量的
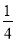 ,该公司应拿出多少辆该品牌平衡车促销才能使这批车的销售利润最大?并求出最大利润.
,该公司应拿出多少辆该品牌平衡车促销才能使这批车的销售利润最大?并求出最大利润. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,AB=12,AD=18,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,BG=
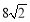 ,则△CEF的周长是 .
,则△CEF的周长是 .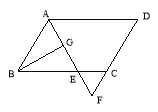
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,经过点A(0,﹣4)的抛物线y=
 x2+bx+c与x轴相交于B(﹣2,0),C两点,O为坐标原点;
x2+bx+c与x轴相交于B(﹣2,0),C两点,O为坐标原点;(1)求抛物线的解析式并用配方法求顶点M的坐标;
(2)若抛物线上有一点P,使∠PCB=∠ABC,求P点坐标;
(3)将抛物线y=
 x2+bx+c向上平移
x2+bx+c向上平移 个单位长度,再向左平移m(m>0)个单位长度得到新抛物线,若新抛物线的顶点M在△ABC内,直接写出m的取值范围.
个单位长度,再向左平移m(m>0)个单位长度得到新抛物线,若新抛物线的顶点M在△ABC内,直接写出m的取值范围.
相关试题

