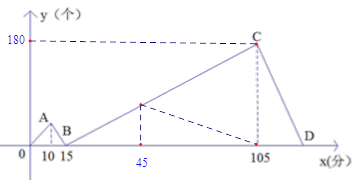
【题目】甲,乙两人同时各接受了600个零件的加工任务,甲比乙每分钟加工的数量多,两人同时开始加工,加工过程中其中一人因故障停止加工几分钟后又继续按原速加工,直到他们完成任务,如图表示甲比乙多加工的零件数量![]() (个)与加工时间
(个)与加工时间![]() (分)之间的函数关系,观察图象解决下列问题:
(分)之间的函数关系,观察图象解决下列问题:
(1)点B的坐标是________,B点表示的实际意义是___________ _____;
(2)求线段BC对应的函数关系式和D点坐标;
(3)乙在加工的过程中,多少分钟时比甲少加工100个零件?
(4)为了使乙能与甲同时完成任务,现让丙帮乙加工,直到完成.丙每分钟能加工3个零件,并把丙加工的零件数记在乙的名下,问丙应在第多少分钟时开始帮助乙?并在图中用虚线画出丙帮助后y与x之间的函数关系的图象.

参考答案:
【答案】(1)B(15,0),甲乙两人工作15分钟时,加工零件的数量相同
(2)y=2x-30,D(150,0)(3)65分钟或125分钟(4)第45分钟
【解析】试题分析:(1)观察图象即可得出点B的坐标,然后根据纵坐标的意义可知此时两人加工的零件数量相同;
(2)利用待定系数法即可得BC对应的函数关系式,根据图象可知105分钟时甲完成任务,甲实际用了100分钟完成任务,从而得到甲的速度,继而知道乙的速度,从而得出点D坐标;
(3)求出CD段的解析式,分别所y=100代入BC、CD段解析式即可得;
(4)设丙应该在x分钟时加入,根据等量关系:乙x分钟加工的数量+乙、丙(105-x)分钟加工的数量=600,解方程即可得,然后补全图象即可.
试题解析:(1)由图象可知B(15,0),根据纵轴表示甲比乙多加工的零件数量可知此时甲、乙加工的零件数量相同,
故答案为:(15,0),甲乙两人工作15分钟时,加工零件的数量相同;
(2)设直线BC的解析式为:y=kx+b,由题意则有
![]() ,解得:
,解得: ![]() ,所以BC段的函数关系式为:y=2x-30,
,所以BC段的函数关系式为:y=2x-30,
由图象可知105分钟时甲完成了任务,甲中间休息了5分钟,105-5=100,
600÷100=6,6-2=4,600÷4=150,所以D(150,0);
(3)把y=100代入y=2x-30,得:100=2x-30,解得:x=65,
设直线CD的解析式为:y=ax+e,由题意则有
![]() ,解得:
,解得: ![]() ,所以BC的函数关系式为:y=-4x+600,
,所以BC的函数关系式为:y=-4x+600,
当y=100时,有100=-4x+600,解得:x=125,
所以乙在加工的过程中,65或125分钟时比甲少加工100个零件;
(4)设x分钟时丙加入,则有:4x+(4+3)(105-x)=600,解得:x=45,
即:丙在45分钟时开始帮助乙,
图象如图所示:
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C是线段AB上一点,△ACD和△BCE都是等边三角形,连结AE,BD,设AE交CD于点F.
(1)求证:△ACE≌△DCB;
(2)求证:△ADF∽△BAD.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,从①∠1=∠2 ②∠C=∠D ③∠A=∠F 三个条件中选出两个作为已知条件,另一个作为结论所组成的命题中,正确命题的个数为( )

A. 0 B. 1 C. 2 D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系中,点A的坐标为(2,4),点B的坐标为(2,7) ,直线l经过A点且平行于x
轴,直线l上的动点C从A点出发以每秒4个单位的速度沿直线l运动.若在x轴上有两点D、E,
连接DB、OB,连接EC、OC,满足DB=OB,EC=OC,设点C运动时间t秒,
(1) 如图1,若动点C从A点出发向左运动,当t=1秒时,
①求线段BC的长和点E的坐标;
②求此时DE与AC的数量关系?
(2)探究:动点C在直线l运动,无论t取何值,是否都存在上述(1)②中的数量关系? 若存在,请证明;若不存在,请说明理由.


图1 图2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠C=90°,AC=3,BC=4,点D是AB的中点,点E在DC的延长线上,且CE=
 CD,过点B作BF∥DE交AE的延长线于点F,交AC的延长线于点G.
CD,过点B作BF∥DE交AE的延长线于点F,交AC的延长线于点G.(1)求证:AB=BG;
(2)若点P是直线BG上的一点,试确定点P的位置,使△BCP与△BCD相似.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中正确的有()
(1) 钝角的补角一定是锐角
(2) 过己知直线外一点作这条直线的垂线有且只有一条
(3) —个角的两个邻补角是对顶角
(4) 等角的补角相等
(5) 直线
 外一点A与直线
外一点A与直线 上各点连接而成的所有线段中,最短线段的长是3cm,则
上各点连接而成的所有线段中,最短线段的长是3cm,则点A到直线
 的距离是3cm .
的距离是3cm .A. 2个 B. 3个 C. 4 个 D. 5 个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=1,BC=
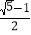 ,在AC边上截取AD=BC,连接BD.
,在AC边上截取AD=BC,连接BD.(1)通过计算,判断AD2与ACCD的大小关系;
(2)求∠ABD的度数.

相关试题

