【题目】根据图中给出的数轴解答问题:
![]()
(1)请你根据图中A,B两点的位置,分别写出他们所表示的有理数为 ;
(2)观察数轴,与点A的距离为4的点表示的数是 ;
(3)如果将数轴折叠,使得点A与表示﹣2的点重合,则点B与表示数 的点重合;
(4)如果数轴上M,N两点之间的距离为2020(M在N的左侧),且M,N两点经过(3)中折叠后互相重合,则M,N两点所表示的数分别是 , .![]()
参考答案:
【答案】(1)1,﹣2.5;(2)﹣3或5;(3)1.5;(4)﹣1010.5,1009.5.
【解析】
(1)(2)观察数轴,直接得出结论;
(3)A点与-2表示的点相距3个单位,其对称点为-0.5,由此得出与B点重合的点;
(4)对称点为-0.5,M点在对称点左边,距离对称点2020÷2=1010个单位,N点在对称点右边,离对称点1010个单位,由此求出M、N两点表示的数.
(1)由数轴可知,A点表示数1,B点表示数﹣2.5.
(2)A点表示数1,与点A的距离为4的点表示的数是:﹣3或5.
(3)当A点与﹣2表示的点重合,则B点与数1.5表示的点重合.
(4)由对称点为﹣0.5,且M、N两点之间的距离为2020(M在N的左侧)可知,
点M、N到﹣1的距离为2020÷2=1010,
所以,M点表示数﹣0.5﹣1010=﹣1010.5,N点表示数﹣0.5+1010=1009.5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)
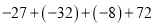
(2)(+6)-(+12)+(+9.6)-(+7.6)
(3)5×
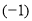 ―
―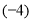 ×
×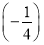
(4)(
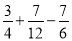 )×(-60 )
)×(-60 )(5)(2
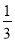 )-(+10
)-(+10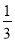 )+(-8
)+(-8 )-(+3)
)-(+3) (6)﹣14﹣(1﹣0.5)×
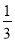 ×[1﹣(﹣2)2];
×[1﹣(﹣2)2]; -
科目: 来源: 题型:
查看答案和解析>>【题目】新的交通法规实施后,驾校的考试规则也发生了变化,考试共设四个科目:科目1、科目2、科目3和科目4,以下简记为:1、2、3、4.四个科目考试在同一地点进行,但每个学员每次只能够参加一个科目考试.在某次考试中,对该考点各科目考试人数进行了调查统计,并根据调查结果绘制成如图所示的条形统计图和扇形统计图(未完成),请结合图中所给信息解答下列问题:
(1)本次被调查的学员共有 人;在被调查者中参加“科目3”测试的有 人;将条形统计图补充完整;
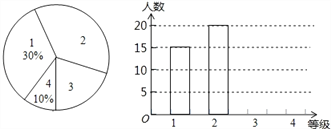
(2)该考点参加“科目4”考试的学员里有3位是教师,某新闻部门准备在该考点参加“科目4”考试的学员中随机选出2位,调查他们对新规的了解情况,请你用列表法或画树状图的方法求出所选两位学员恰好都是教师的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】你会玩“24点”游戏吗?从一副扑克牌(去掉大、小王)中任意抽取4张,根据牌面上的数字,添加+、一、×、÷和括号等符号进行运算,每张牌只能用一次,使得运算结果为24,其中A、J、Q、K分别代表1,11,12,13.
(1)小明抽到的是如下4张牌,你凑成24的算式是______(写出一个即可).

(2)现有四个有理数3、4、 -6、10,运用上述规则写出两种不同方法的运算式,使其结果等于24.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为响应国家的“节能减排”政策,某厂家开发了一种新型的电动车,如图,它的大灯A射出的光线AB、AC与地面MN的夹角分别为22°和31°,AT⊥MN,垂足为T,大灯照亮地面的宽度BC的长为
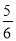 m.
m.(1)求BT的长(不考虑其他因素).
(2)一般正常人从发现危险到做出刹车动作的反应时间是0.2s,从发现危险到电动车完全停下所行驶的距离叫做最小安全距离.某人以20km/h的速度驾驶该车,从做出刹车动作到电动车停止的刹车距离是
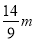 ,请判断该车大灯的设计是否能满足最小安全距离的要求(大灯与前轮前端间水平距离忽略不计),并说明理由.
,请判断该车大灯的设计是否能满足最小安全距离的要求(大灯与前轮前端间水平距离忽略不计),并说明理由.(参考数据:sin22°≈
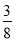 ,tan22°≈
,tan22°≈ ,sin31°≈
,sin31°≈ ,tan31°≈
,tan31°≈ )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某花店准备购进甲、乙两种花卉,若购进甲种花卉20盆,乙种花卉50盆,需要720元;若购进甲种花卉40盆,乙种花卉30盆,需要880元.
(1)求购进甲、乙两种花卉,每盆各需多少元?
(2)该花店销售甲种花卉每盆可获利6元,销售乙种花卉每盆可获利1元,现该花店准备拿出800元全部用来购进这两种花卉,设购进甲种花卉x盆,全部销售后获得的利润为W元,求W与x之间的函数关系式;
(3)在(2)的条件下,考虑到顾客需求,要求购进乙种花卉的数量不少于甲种花卉数量的6倍,且不超过甲种花卉数量的8倍,那么该花店共有几种购进方案?在所有的购进方案中,哪种方案获利最大?最大利润是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠C=90°,AC=3,AB=5,点O在BC边的中线AD上,⊙O与BC相切于点E,且∠OBA=∠OBC.
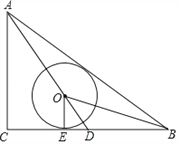
(1)求证:AB为⊙O的切线;
(2)求⊙O的半径;
(3)求tan∠BAD.
相关试题

