【题目】如图,△ABC中,∠C=90°,AC=3,AB=5,点O在BC边的中线AD上,⊙O与BC相切于点E,且∠OBA=∠OBC.
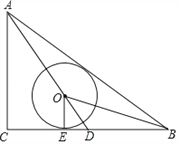
(1)求证:AB为⊙O的切线;
(2)求⊙O的半径;
(3)求tan∠BAD.
参考答案:
【答案】(1)详见解析;(2)⊙O的半径为![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)作OF垂直AB于点F,然后根据角平分线的性质定理即可证得OE=OF,从而证得结论;
(2)根据勾股定理求得![]() ,进而求得
,进而求得![]() 设
设![]() 的半径为r,然后根据
的半径为r,然后根据![]() 得到
得到![]()
解关于r的方程即可求得半径;
(3)证得Rt△ODE∽Rt△ADC,根据相似三角形的性质求得![]() ,
,
即可求得![]() ,
, ![]() ,解直角三角形即可求得
,解直角三角形即可求得![]() .
.
试题解析:
(1)证明:如图,作OF垂直AB于点F,
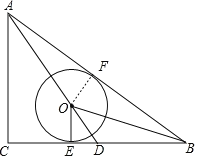
∵⊙O与BC相切于点E,
∴OE⊥BC,
又∠OBA=∠OBC,
∴OE=OF,
∴AB为![]() 的切线 ;
的切线 ;
(2)∵∠C=90,AC=3,AB=5,
![]() 又D为BC的中点,
又D为BC的中点,
∴CD=DB=2,
![]()
设⊙O的半径为r,即
![]()
∴6+2r+5r=12
![]()
∴⊙O的半径为![]()
(3) ![]() ,OE⊥BC,
,OE⊥BC,
∴OE∥AC,
∴Rt△ODE∽Rt△ADC,
∴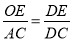 ,∴
,∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据图中给出的数轴解答问题:
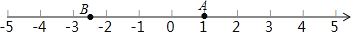
(1)请你根据图中A,B两点的位置,分别写出他们所表示的有理数为 ;
(2)观察数轴,与点A的距离为4的点表示的数是 ;
(3)如果将数轴折叠,使得点A与表示﹣2的点重合,则点B与表示数 的点重合;
(4)如果数轴上M,N两点之间的距离为2020(M在N的左侧),且M,N两点经过(3)中折叠后互相重合,则M,N两点所表示的数分别是 , .

-
科目: 来源: 题型:
查看答案和解析>>【题目】为响应国家的“节能减排”政策,某厂家开发了一种新型的电动车,如图,它的大灯A射出的光线AB、AC与地面MN的夹角分别为22°和31°,AT⊥MN,垂足为T,大灯照亮地面的宽度BC的长为
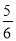 m.
m.(1)求BT的长(不考虑其他因素).
(2)一般正常人从发现危险到做出刹车动作的反应时间是0.2s,从发现危险到电动车完全停下所行驶的距离叫做最小安全距离.某人以20km/h的速度驾驶该车,从做出刹车动作到电动车停止的刹车距离是
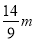 ,请判断该车大灯的设计是否能满足最小安全距离的要求(大灯与前轮前端间水平距离忽略不计),并说明理由.
,请判断该车大灯的设计是否能满足最小安全距离的要求(大灯与前轮前端间水平距离忽略不计),并说明理由.(参考数据:sin22°≈
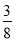 ,tan22°≈
,tan22°≈ ,sin31°≈
,sin31°≈ ,tan31°≈
,tan31°≈ )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某花店准备购进甲、乙两种花卉,若购进甲种花卉20盆,乙种花卉50盆,需要720元;若购进甲种花卉40盆,乙种花卉30盆,需要880元.
(1)求购进甲、乙两种花卉,每盆各需多少元?
(2)该花店销售甲种花卉每盆可获利6元,销售乙种花卉每盆可获利1元,现该花店准备拿出800元全部用来购进这两种花卉,设购进甲种花卉x盆,全部销售后获得的利润为W元,求W与x之间的函数关系式;
(3)在(2)的条件下,考虑到顾客需求,要求购进乙种花卉的数量不少于甲种花卉数量的6倍,且不超过甲种花卉数量的8倍,那么该花店共有几种购进方案?在所有的购进方案中,哪种方案获利最大?最大利润是多少元?
-
科目: 来源: 题型:
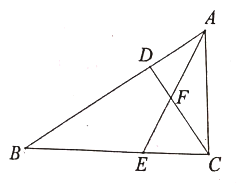
查看答案和解析>>【题目】已知:如图,在
 中,
中,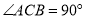 ,
,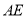 是角平分线,
是角平分线,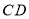 是高,
是高,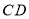 和
和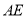 交于点
交于点 .
.
(1)若
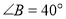 ,则
,则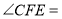 ____________
____________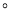 ,
,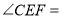 ____________
____________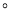 ;
;(2)结合(1)中的结果,探究
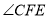 和
和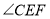 的关系,并说明理由.
的关系,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】泰兴市为进一步改善生态环境决定对街道进行绿化建设,为此准备购进甲、乙两种树木、已知甲种树木的单价为
 元,乙种树木的单价为
元,乙种树木的单价为 元.
元.(1)若
 街道购买甲、乙两种树木共花费
街道购买甲、乙两种树木共花费 元,其中,乙种树木是甲种树木的一半多
元,其中,乙种树木是甲种树木的一半多 棵,请求出该街道购买的甲、乙两种树木各多少棵;
棵,请求出该街道购买的甲、乙两种树木各多少棵;(2)相关资料表明:甲种树木的成活率为
 ,乙种树木的成活率为
,乙种树木的成活率为 .现
.现 街道购买甲、乙两种树木共
街道购买甲、乙两种树木共 棵,为了使这批树木的总成活率不低于
棵,为了使这批树木的总成活率不低于 ,则甲种树木至多购买多少棵?
,则甲种树木至多购买多少棵? -
科目: 来源: 题型:
查看答案和解析>>【题目】对某一个函数给出如下定义:若存在实数
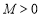 ,对于任意的函数值
,对于任意的函数值 ,都满足
,都满足 ,则称这个函数是有界函数,在所有满足条件的
,则称这个函数是有界函数,在所有满足条件的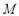 中,其最小值称为这个函数的边界值.例如,下图中的函数是有界函数,其边界值是1.
中,其最小值称为这个函数的边界值.例如,下图中的函数是有界函数,其边界值是1.
(1)分别判断函数

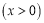 和
和 是不是有界函数?若是有界函数,求其边界值;
是不是有界函数?若是有界函数,求其边界值;(2)若函数
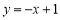
 的边界值是2,且这个函数的最大值也是2,求
的边界值是2,且这个函数的最大值也是2,求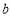 的取值范围;
的取值范围;(3)将函数
 的图象向下平移
的图象向下平移 个单位,得到的函数的边界值是
个单位,得到的函数的边界值是 ,当
,当 在什么范围时,满足
在什么范围时,满足 ?
?
相关试题

