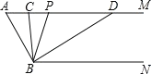
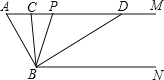
【题目】如图,已知AM∥BN,∠A=80°,点P是射线AM上的动点(与A不重合),BC、BD分别平分∠ABP和∠PBN,交射线AM于点C、D.
(1)求∠CBD的度数;
(2)当点P运动时,∠APB∶∠ADB的度数比值是否随之发生变化?若不变,请求出这个比值;若变化,请找出变化规律.
(3)当点P运动到使∠ACB=∠ABD时,求∠ABC的度数.
参考答案:
【答案】(1)50°;(2)不变,∠APB:∠ADB=2:1,理由详见解析;(3)∠ABC=25°.
【解析】
(1)先根据平行线的性质求出∠ABN,然后再根据角平分线的定义即可求出∠CBD;
(2)先根据平行线的性质可得∠APB=∠PBN、∠ADB=∠DBN,然后再由角平分线的定义即可发现规律;
(3)由平行线的性质可得∠ACB=∠CBN=50°+∠DBN,再结合条件可得到∠DBN=∠ABC,且∠ABC+∠DBN=60°,即可求解.
解:(1)∵AM∥BN,
∴∠ABN+∠A=180°,
又∵∠A=80°,
∴∠ABN=180°-80°=100°,
∴∠ABP+∠PBN=100°,
∵BC平分∠ABP,BD平分∠PBN,
∴∠ABP=2∠CBP,∠PBN=2∠DBP,
∴2∠CBP+2∠DBP=100°,
∴∠CBD=∠CBP+∠DBP=50°;
(2)不变,∠APB:∠ADB=2:1.
∵AM∥BN,
∴∠APB=∠PBN,∠ADB=∠DBN,
∵BD平分∠PBN,
∴∠PBN=2∠DBN,
∴∠APB:∠ADB=2:1;
(3)∵AM∥BN,
∴∠ACB=∠CBN,
当∠ACB=∠ABD时,则有∠CBN=∠ABD,
∴∠ABC+∠CBD=∠CBD+∠DBN,
∴∠ABC=∠DBN,
由(1)可知∠ABN=100°,∠CBD=50°,
∴∠ABC+∠DBN=50°,
∴∠ABC=25°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=4x与反比例函数y=
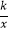 (k≠0)相交与点A(1,a),B是反比例函数图象上一点,直线OB与x轴的夹角为α,且tanα=
(k≠0)相交与点A(1,a),B是反比例函数图象上一点,直线OB与x轴的夹角为α,且tanα=  .
.
(1)求k的值.
(2)求点B的坐标.
(3)设点P点在y轴上,若△PAB是以AB为直角边的直角三角形,则点P的坐标为: . -
科目: 来源: 题型:
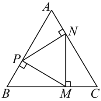
查看答案和解析>>【题目】如图,点P,M,N分别在等边△ABC的各边上,且MP⊥AB,MN⊥BC,PN⊥AC.
(1)求证:△PMN是等边三角形;
(2)若AB=9 cm,求CM的长度.
-
科目: 来源: 题型:
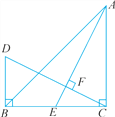
查看答案和解析>>【题目】如图,△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF.
(1)求证:BF=2AE;
(2)若CD=
 ,求AD的长.
,求AD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合与实践:在学习了《7.4实践与探索》之后,小亮买了若干块完全相同的长方形拼图(图1),第一次他用2块图1的长方形拼出了图2所示的正方形,第二次他又用4块图1的长方形拼出了图3所示的正方形(中间留有一个正方形小洞,即阴影区域),经过测量,他发现图3的大正方形的边长为
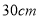 .
.
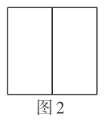

(1)请你帮小亮求出图1中长方形的长和宽;
(2)请你参照图3,用图1的长方形拼出一个面积为
 的正方形(中间留有一个正方形小洞),请画出你拼出的大正方形(要求画出两个).
的正方形(中间留有一个正方形小洞),请画出你拼出的大正方形(要求画出两个). -
科目: 来源: 题型:
查看答案和解析>>【题目】疫情期间,为减少交叉感染,催生了以智能技术为支撑的无接触服务.某快递公司准备购进
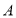 ,
, 两种型号的智能机器人送快递.经市场调査发现,
两种型号的智能机器人送快递.经市场调査发现,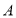 型号机器人的单价比
型号机器人的单价比 型号机器人贵600元,3台
型号机器人贵600元,3台 型号机器人比2台
型号机器人比2台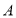 型号机器人贵1200元.
型号机器人贵1200元.(1)求
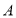 ,
, 两种型号机器人的单价各是多少元?
两种型号机器人的单价各是多少元?(2)若该快递公司准备用不超过132000元购进
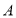 ,
, 两种型号机器人共50台,请问该快递公司最多可购进
两种型号机器人共50台,请问该快递公司最多可购进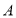 型号机器人多少台?
型号机器人多少台? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,AC=BC,AE是BC边上的中线,过点C作AE 的垂线CF,垂足为F,过点B作BD⊥BC,交CF的延长线于点D.
(1)求证:AE=CD.
(2)若AC=12 cm,求BD的长.
相关试题

