【题目】如图,直线y=4x与反比例函数y= ![]() (k≠0)相交与点A(1,a),B是反比例函数图象上一点,直线OB与x轴的夹角为α,且tanα=
(k≠0)相交与点A(1,a),B是反比例函数图象上一点,直线OB与x轴的夹角为α,且tanα= ![]() .
.
(1)求k的值.
(2)求点B的坐标.
(3)设点P点在y轴上,若△PAB是以AB为直角边的直角三角形,则点P的坐标为: .
参考答案:
【答案】
(1)解:把点A(1,a)代入y=4x中,得a=4,
所以A(1,4),
把点A(1,4)代入 ![]() 中,得k=4;
中,得k=4;
(2)解:过点B作BE垂直于x轴于点E,如图示,
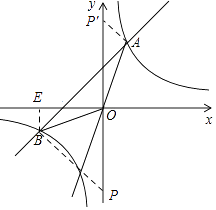
设BE长为m,在Rt△OBE中,
∵ ![]() ,
,
∴ ![]() ,即 OE=4BE=4m,
,即 OE=4BE=4m,
∴所以点B坐标为(﹣m,﹣4m),
把点B代入 ![]() 中,
中,
得:4m2=4,
解得m1=1,m2=﹣1(舍去)
∴点B坐标为(﹣4,﹣1);
(3)(0,5)或(0,﹣5)
【解析】解: (3)如图所示,过A作AP'⊥AB,交y轴于P',过B作BP⊥AB,交y轴于P,
根据A(1,4),B(﹣4,﹣1),可得直线AB的解析式为y=x+3;
根据直角坐标系中互相垂直的两直线的系数k互为负倒数,
可设直线BP为y=﹣x+m,
把B(﹣4,﹣1)代入可得,m=﹣5;
设直线AP'的解析式为y=﹣x+n,
把A(1,4)代入,可得n=5,
∴点P坐标为:(0,5),(0,﹣5).
所以答案是:(0,5)或(0,﹣5).
【考点精析】本题主要考查了解直角三角形的相关知识点,需要掌握解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知12+22+32+…+n2=
 n(n+1)(2n+1)(n为正整数).
n(n+1)(2n+1)(n为正整数).求22+42+62+…+502的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长青化工厂与A、B两地有公路、铁路相连.这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8000元的产品运到B地.已知公路运价为1.5元/(吨·千米),铁路运价为1.2元/(吨·千米),且这两次运输共支出公路运输费15000元,铁路运输费97200元.

求:(1)该工厂从A地购买了多少吨原料?制成运往B地的产品多少吨?
(2)这批产品的销售款比原料费与运输费的和多多少元?
-
科目: 来源: 题型:
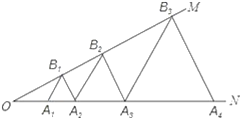
查看答案和解析>>【题目】如图,已知:∠MON=30°,点A1、A2、A3 在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=a,则△A6B6A7的边长为______.
-
科目: 来源: 题型:
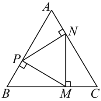
查看答案和解析>>【题目】如图,点P,M,N分别在等边△ABC的各边上,且MP⊥AB,MN⊥BC,PN⊥AC.
(1)求证:△PMN是等边三角形;
(2)若AB=9 cm,求CM的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF.
(1)求证:BF=2AE;
(2)若CD=
 ,求AD的长.
,求AD的长.
-
科目: 来源: 题型:
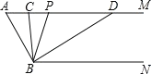
查看答案和解析>>【题目】如图,已知AM∥BN,∠A=80°,点P是射线AM上的动点(与A不重合),BC、BD分别平分∠ABP和∠PBN,交射线AM于点C、D.
(1)求∠CBD的度数;
(2)当点P运动时,∠APB∶∠ADB的度数比值是否随之发生变化?若不变,请求出这个比值;若变化,请找出变化规律.
(3)当点P运动到使∠ACB=∠ABD时,求∠ABC的度数.
相关试题

