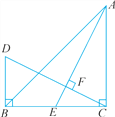
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,AE是BC边上的中线,过点C作AE 的垂线CF,垂足为F,过点B作BD⊥BC,交CF的延长线于点D.
(1)求证:AE=CD.
(2)若AC=12 cm,求BD的长.
参考答案:
【答案】(1)证明见解析(2)6cm
【解析】(1)证两条线段相等,通常用全等,本题中的AE和CD分别在三角形AEC和三角形CDB中,在这两个三角形中,已经有一组边相等,一组角相等了,因此只需再找一组角即可利用角角边进行解答.
(2)由(1)得BD=EC=![]() BC=
BC=![]() AC,且AC=12,即可求出BD的长.
AC,且AC=12,即可求出BD的长.
(1)证明:∵DB⊥BC,CF⊥AE,
∴∠DCB+∠D=∠DCB+∠AEC=90°.
∴∠D=∠AEC.
又∵∠DBC=∠ECA=90°,
且BC=CA,
∴△DBC≌△ECA(AAS).
∴AE=CD.
(2)解:由(1)得AE=CD,AC=BC,
∴△CDB≌△AEC(HL),
∴BD=CE,
∵AE是BC边上的中线,
∴BD=EC=![]() BC=
BC=![]() AC,且AC=12cm.
AC,且AC=12cm.
∴BD=6cm.
-
科目: 来源: 题型:
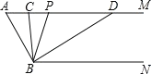
查看答案和解析>>【题目】如图,已知AM∥BN,∠A=80°,点P是射线AM上的动点(与A不重合),BC、BD分别平分∠ABP和∠PBN,交射线AM于点C、D.
(1)求∠CBD的度数;
(2)当点P运动时,∠APB∶∠ADB的度数比值是否随之发生变化?若不变,请求出这个比值;若变化,请找出变化规律.
(3)当点P运动到使∠ACB=∠ABD时,求∠ABC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合与实践:在学习了《7.4实践与探索》之后,小亮买了若干块完全相同的长方形拼图(图1),第一次他用2块图1的长方形拼出了图2所示的正方形,第二次他又用4块图1的长方形拼出了图3所示的正方形(中间留有一个正方形小洞,即阴影区域),经过测量,他发现图3的大正方形的边长为
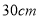 .
.

(1)请你帮小亮求出图1中长方形的长和宽;
(2)请你参照图3,用图1的长方形拼出一个面积为
 的正方形(中间留有一个正方形小洞),请画出你拼出的大正方形(要求画出两个).
的正方形(中间留有一个正方形小洞),请画出你拼出的大正方形(要求画出两个). -
科目: 来源: 题型:
查看答案和解析>>【题目】疫情期间,为减少交叉感染,催生了以智能技术为支撑的无接触服务.某快递公司准备购进
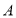 ,
, 两种型号的智能机器人送快递.经市场调査发现,
两种型号的智能机器人送快递.经市场调査发现,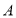 型号机器人的单价比
型号机器人的单价比 型号机器人贵600元,3台
型号机器人贵600元,3台 型号机器人比2台
型号机器人比2台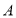 型号机器人贵1200元.
型号机器人贵1200元.(1)求
 ,
, 两种型号机器人的单价各是多少元?
两种型号机器人的单价各是多少元?(2)若该快递公司准备用不超过132000元购进
 ,
, 两种型号机器人共50台,请问该快递公司最多可购进
两种型号机器人共50台,请问该快递公司最多可购进 型号机器人多少台?
型号机器人多少台? -
科目: 来源: 题型:
查看答案和解析>>【题目】具备下列条件的三角形中,不是直角三角形的是( )
A. ∠A+∠B=∠C B. ∠B=∠C=
 ∠A
∠AC. ∠A=90°-∠B D. ∠A-∠B=90°
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,△ABC为等边三角形,AE=CD,AD、BE相交于点P.

(1)求证:△AEB≌△CDA;
(2)求∠BPQ的度数;
(3)若BQ⊥AD于Q,PQ=6,PE=2,求BE的长.
-
科目: 来源: 题型:
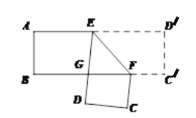
查看答案和解析>>【题目】如图,把一张两边分别平行的纸条折成如图所示,EF为折痕,ED交BF于点G,且∠EFB=48°,则下列结论: ①∠DEF=48°;②∠AED=84°;③∠BFC=84°;④∠DGF=96°,其中正确的个数有( )
A. 4个B. 3个C. 2个D. 1个
相关试题

