【题目】如图,四边形ABCD为菱形,点E为对角线AC上的一个动点,连结DE并延长交AB于点F,连结BE.
(1)如果①,求证:∠AFD=∠EBC;
(2)如图②,若DE=EC且BE⊥AF,求∠DAB的度数;
(3)若∠DAB=90°且当△BEF为等腰三角形时,求∠EFB的度数(只写出条件与对应的结果)

参考答案:
【答案】(1)干劲儿目前并解析;(2)60°;(3)30°或120°.
【解析】
试题分析:(1)直接利用全等三角形的判定方法得出△DCE≌△BCE(SAS),即可得出答案;
(2)利用等腰三角形的性质结合垂直的定义得出∠DAB的度数;
(3)利用正方形的性质结合等腰三角形的性质得出①当F在AB延长线上时,以及②当F在线段AB上时,分别求出即可.
试题解析:(1)∵四边形ABCD为菱形,
∴DC=CB,
在△DCE和△BCE中,
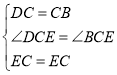 ,
,
∴△DCE≌△BCE(SAS),
∴∠EDC=∠EBC,
∵DC∥AB,
∴∠EDC=∠AFD,
∴∠AFD=∠EBC;
(2)∵DE=EC,
∴∠EDC=∠ECD,
设∠EDC=∠ECD=∠CBE=x°,则∠CBF=2x°,
由BE⊥AF得:2x+x=90°,
解得:x=30°,
∴∠DAB=∠CBF=60°;
(3)分两种情况:
①如图1,当F在AB延长线上时,

∵∠EBF为钝角,
∴只能是BE=BF,设∠BEF=∠BFE=x°,
可通过三角形内角形为180°得:
90+x+x+x=180,
解得:x=30,
∴∠EFB=30°;
②如图2,当F在线段AB上时,
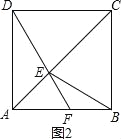
∵∠EFB为钝角,
∴只能是FE=FB,设∠BEF=∠EBF=x°,则有∠AFD=2x°,
可证得:∠AFD=∠FDC=∠CBE,
得x+2x=90,
解得:x=30,
∴∠EFB=120°,
综上:∠EFB=30°或120°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若m2+m-1=0,则m3+2m2+2018的值为( )
A. 2020 B. 2017 C. 2019 D. 2015
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二元一次方程2x﹣y=3,用含x的式子表示y的形式是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=2.将△ABC绕点C按顺时针方向旋转n度后得到△EDC,此时点D落在AB边上,斜边DE交AC于点F,则n的大小和图中阴影部分的面积分别为( )

A. 30,2 B. 60,2 C. 60,
 D. 60,
D. 60, 
-
科目: 来源: 题型:
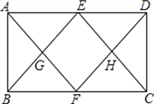
查看答案和解析>>【题目】如图,在矩形ABCD中,E,F分别为AD,BC的中点,连结AF,DF,BE,CE,AF与BE交于G,DF与CE交于H.求证:四边形EGFH为菱形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm.动点M从点B出发,在BA边上以每秒3cm的速度向定点A运动,同时动点N从点C出发,在CB边上以每秒2cm的速度向点B运动,运动时间为t秒(0<t<
 ),连接MN.
),连接MN.(1)若△BMN与△ABC相似,求t的值;
(2)连接AN,CM,若AN⊥CM,求t的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC,按如下步骤作图:
①分别以A,C为圆心,大于
 的长为半径画弧,两弧交于P,Q两点;
的长为半径画弧,两弧交于P,Q两点; ②作直线PQ,分别交AB,AC于点E,D,连接CE;
③过C作CF∥AB交PQ于点F,连接AF.
(1)求证:△AED≌△CFD;
(2)求证:四边形AECF是菱形.

相关试题

