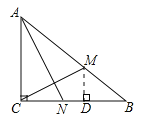
【题目】如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm.动点M从点B出发,在BA边上以每秒3cm的速度向定点A运动,同时动点N从点C出发,在CB边上以每秒2cm的速度向点B运动,运动时间为t秒(0<t<![]() ),连接MN.
),连接MN.
(1)若△BMN与△ABC相似,求t的值;
(2)连接AN,CM,若AN⊥CM,求t的值.

参考答案:
【答案】(1)△BMN与△ABC相似时,t的值为![]() 或
或![]() ;(2)t=
;(2)t=![]()
【解析】试题分析:(1)由题意得出BM,CN, BN,BA,分两种情况讨论:①当△BMN∽△BAC时,利用相似三角形的性质得![]() ,解出t;②当△BMN∽△BCA时,
,解出t;②当△BMN∽△BCA时, ![]() ,解出t;
,解出t;
(2)过点M作MD⊥CB于点D,得到DM,BD,由BM=3tcm,CN=2tcm,得到CD,利用三角形相似的判定定理得△CAN∽△DCM,由三角形相似的性质得![]() ,解出t.
,解出t.
试题解析:(1)由题意知,BM=3tcm,CN=2tcm,∴BN=(8﹣2t)cm,BA=![]() =10(cm),当△BMN∽△BAC时,
=10(cm),当△BMN∽△BAC时, ![]() ,∴
,∴![]() ,解得:t=
,解得:t=![]() ;
;
当△BMN∽△BCA时, ![]() ,∴
,∴![]() ,解得:t=
,解得:t=![]() ,
,
∴△BMN与△ABC相似时,t的值为![]() 或
或![]() ;
;
(2)过点M作MD⊥CB于点D,由题意得:DM=BMsinB=![]() =
= ![]() (cm),BD=BMcosB=
(cm),BD=BMcosB=![]() =
= ![]() (cm),BM=3tcm,CN=2tcm,∴CD=(
(cm),BM=3tcm,CN=2tcm,∴CD=(![]() )cm,∵AN⊥CM,∠ACB=90°,∴∠CAN+∠ACM=90°,∠MCD+∠ACM=90°,∴∠CAN=∠MCD,∵MD⊥CB,∴∠MDC=∠ACB=90°,∴△CAN∽△DCM,∴
)cm,∵AN⊥CM,∠ACB=90°,∴∠CAN+∠ACM=90°,∠MCD+∠ACM=90°,∴∠CAN=∠MCD,∵MD⊥CB,∴∠MDC=∠ACB=90°,∴△CAN∽△DCM,∴![]() ,∴
,∴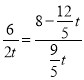 ,解得t=
,解得t=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=2.将△ABC绕点C按顺时针方向旋转n度后得到△EDC,此时点D落在AB边上,斜边DE交AC于点F,则n的大小和图中阴影部分的面积分别为( )

A. 30,2 B. 60,2 C. 60,
 D. 60,
D. 60, 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD为菱形,点E为对角线AC上的一个动点,连结DE并延长交AB于点F,连结BE.
(1)如果①,求证:∠AFD=∠EBC;
(2)如图②,若DE=EC且BE⊥AF,求∠DAB的度数;
(3)若∠DAB=90°且当△BEF为等腰三角形时,求∠EFB的度数(只写出条件与对应的结果)

-
科目: 来源: 题型:
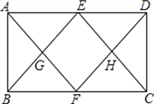
查看答案和解析>>【题目】如图,在矩形ABCD中,E,F分别为AD,BC的中点,连结AF,DF,BE,CE,AF与BE交于G,DF与CE交于H.求证:四边形EGFH为菱形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC,按如下步骤作图:
①分别以A,C为圆心,大于
 的长为半径画弧,两弧交于P,Q两点;
的长为半径画弧,两弧交于P,Q两点; ②作直线PQ,分别交AB,AC于点E,D,连接CE;
③过C作CF∥AB交PQ于点F,连接AF.
(1)求证:△AED≌△CFD;
(2)求证:四边形AECF是菱形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(2﹣3)+(﹣1)的结果是( )
A.﹣2
B.0
C.1
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题正确的是( )
A. 若a>b,b<c,则a>cB. 若a∥b,b∥c,则a∥c
C. 49的平方根是7D. 负数没有立方根
相关试题

