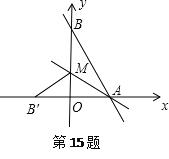
【题目】如图,直线y=﹣![]() x+8与x轴,y轴分别交于点A和B,M是OB上的一点,若将△ABM沿AM折叠,点B恰好落在x轴上的点B′处,则直线AM的解析式为 .
x+8与x轴,y轴分别交于点A和B,M是OB上的一点,若将△ABM沿AM折叠,点B恰好落在x轴上的点B′处,则直线AM的解析式为 .
参考答案:
【答案】y=-0.5x+3
【解析】此题首先分别求出A,B两个点的坐标,得到OA,OB的长度,再根据勾股定理求出AB,再求出OB′,然后根据已知得到BM=B′M,设BM=x,在Rt△B′OM中利用勾股定理求出x,这样可以求出OM,从而求出了M的坐标,最后用待定系数法求直线的解析式.
解:当x=0时,y=8;当y=0时,x=6,
∴OA=6,OB=8,
∴AB=10,
根据已知得到BM=B'M,
AB'=AB=10,
∴OB'=4,设BM=x,则B'M=x,
OM=8﹣x,在直角△B'MO中,x2=(8﹣x)2+42,
∴x=5,
∴OM=3,
∴M(0,3),
设直线AM的解析式为y=kx+b,把M(0,3),A(6,0)代入其中
得:
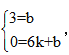
∴k=﹣![]() ,b=3,
,b=3,
∴y=﹣![]() x+3.
x+3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】手机上网已经成为当今年轻人时尚的网络生活,某网络公司看中了这种商机,推出了两种手机上网的计费方式:方式A以每分钟0.1元的价格按上网时间计费;方式B除收月基费20元外,再以每分钟0.06元的价格按上网时间计费.假设某客户月手机上网的时间为x分钟,上网费用为y元.
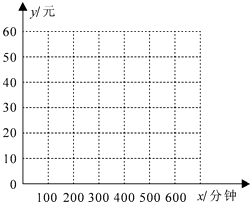
(1)分别写出该客户按A、B两种方式的上网费y(元)与每月上网时间x(分钟)的函数关系式,并在右图的坐标系中画出这两个函数的图象;
(2)如何选择计费方式能使该客户上网费用更合算? -
科目: 来源: 题型:
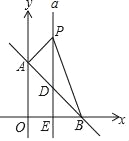
查看答案和解析>>【题目】如图,平面直角坐标系中,直线AB:y=﹣x+b交y轴于点A,交x轴于点B,S△AOB=8.
(1)求点B的坐标和直线AB的函数表达式;
(2)直线a垂直平分OB交AB于点D,交x轴于点E,点P是直线a上一动点,且在点D的上方,设点P的纵坐标为m.
①用含m的代数式表示△ABP的面积;
②当S△ABP=6时,求点P的坐标;
③在②的条件下,在坐标轴上,是否存在一点Q,使得△ABQ与△ABP面积相等?若存在,直接写出点Q的坐标,若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB是⊙O的直径,⊙O过BC的中点D,且DE⊥AC于点E.
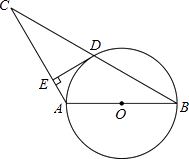
(1)试判断DE与⊙O的位置关系,并证明你的结论;
(2)若∠C=30°,CE=6,求⊙O的半径. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,B、C、E三点在同一条直线上,AC∥DE,AC=CE,∠ACD=∠B.
(1)求证:BC=DE
(2)若∠A=40°,求∠BCD的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】随着人们环保意识的不断增强,我市家庭电动自行车的拥有量逐年增加.据统计,某小区2009年底拥有家庭电动自行车125辆,2011年底家庭电动自行车的拥有量达到180辆.
(1)若该小区2009年底到2012年底家庭电动自行车拥有量的年平均增长率相同,则该小区到2012年底电动自行车将达到多少辆?
(2)为了缓解停车矛盾,该小区决定投资3万元再建若干个停车位,据测算,建造费用分别为室内车位1000元/个,露天车位200元/个.考虑到实际因素,计划露天车位的数量不少于室内车位的2倍,但不超过室内车位的2.5倍,则该小区最多可建两种车位各多少个?试写出所有可能的方案. -
科目: 来源: 题型:
查看答案和解析>>【题目】“十一”长假期间,小张和小李决定骑自行车外出旅游,两人相约一早从各自家中出发,已知两家相距10千米,小张出发必过小李家.
(1)若两人同时出发,小张车速为20千米,小李车速为15千米,经过多少小时能相遇?
(2)若小李的车速为10千米,小张提前20分钟出发,两人商定小李出发后半小时二人相遇,则小张的车速应为多少?
相关试题

