【题目】初三年级的一场篮球比赛中,如图队员甲正在投篮,已知球出手时离地面高 ![]() m,与篮圈中心的水平距离为7m,当球出手后水平距离为4m时到达最大高度4m,设篮球运行的轨迹为抛物线,篮圈距地面3m.
m,与篮圈中心的水平距离为7m,当球出手后水平距离为4m时到达最大高度4m,设篮球运行的轨迹为抛物线,篮圈距地面3m.
(1)建立如图所示的平面直角坐标系,求抛物线的解析式并判断此球能否准确投中?
(2)此时,若对方队员乙在甲前面1m处跳起盖帽拦截,已知乙的最大摸高为3.1m,那么他能否获得成功?
参考答案:
【答案】
(1)解:由题意可知,抛物线经过(0, ![]() ),顶点坐标是(4,4).
),顶点坐标是(4,4).
∴可设抛物线的解析式是 ![]() ,
,
代入点(0, ![]() ),得:
),得: ![]() ,解得
,解得 ![]() ,
,
∴抛物线的解析式是 ![]() ;
;
∵当 ![]() 时,
时, ![]() ,
,
∴代表篮圈的点(7,3)在抛物线上,
∴能够投中
(2)解:∵当 ![]() 时,
时, ![]() <3.1,
<3.1,
∴乙能够盖帽拦截成功
【解析】(1)根据题意可知抛物线的顶点坐标,及抛物线过(0, ![]() ),设函数解析式为顶点式,再利用待定系数法求出函数解析式,然后将x=7代入函数解析式,若y=3,说明能投中,否则不能。
),设函数解析式为顶点式,再利用待定系数法求出函数解析式,然后将x=7代入函数解析式,若y=3,说明能投中,否则不能。
(2)将x=1代入函数解析式求出对应的函数值,再与3.1比较大小即可。
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中:①过一点有且只有一条直线与已知直线平行;②过一点有且只有一条直线与已知直线垂直;③垂直于同一直线的两条直线互相平行;④平行于同一直线的两条直线互相平行;⑤两条直线被第三条直线所截,如果同旁内角相等,那么这两条直线互相平行;⑥连结
 、
、 两点的线段就是
两点的线段就是 、
、 两点之间的距离,其中正确的有( )
两点之间的距离,其中正确的有( )A.
 个B.
个B. 个C.
个C. 个D.
个D. 个
个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E是四边形ABCD的对角线BD上一点,且∠BAC=∠BDC=∠DAE.
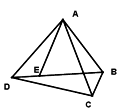
①试说明BE·AD=CD·AE;
②根据图形特点,猜想 可能等于哪两条线段的比?并证明你的猜想,(只须写出有线段的一组即可)
可能等于哪两条线段的比?并证明你的猜想,(只须写出有线段的一组即可) -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中,有四个点A(﹣8,3)、B(﹣4,5)、C(0,n)、D(m,0),当四边形ABCD的周长最短时,求
 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为
 ,点A,B,E在x轴上,若正方形BEFG的边长为6,则C点坐标为( )
,点A,B,E在x轴上,若正方形BEFG的边长为6,则C点坐标为( ) 
A.(3,2)
B.(3,1)
C.(2,2)
D.(4,2) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFGH的一边FG在BC上,顶点E、H分别在AB、AC上,已知BC=40cm,AD=30cm.

(1)求证:△AEH∽△ABC;
(2)求这个正方形的边长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,花丛中有一路灯杆AB,在灯光下,大华在D点处的影长DE=3米,沿BD方向行走到达G点,DG=5米,这时大华的影长GH=5米.如果大华的身高为2米,求路灯杆AB的高度.

相关试题

