搜索
【题目】如图，在平面直角坐标系中，点A、B的坐标分别为（0，4）、（4，0），点C在第一象限内，∠BAC=90°，AB=2AC，函数y=
（x＞0）的图象经过点C，将△ABC沿x轴的正方向向右平移m个单位长度，使点A恰好落在函数y=（x＞0）的图象上，则m的值为（ ）
A. 
B. 
C. 3 D. 
参考答案：
【答案】C
【解析】
如图，过点C作CM⊥y轴于点M，易证△ABO∽△CAM，根据相似三角形的性质及已知条件求得OA、OB的长，即可求得点C的坐标，从而求得反比例函数的解析式，由平移后点A正好在反比例函数的图象上，可得点A的纵坐标，代入解析式即可求得点A 的横坐标，从而求得平移的距离.
如图，过点C作CM⊥y轴于点M，
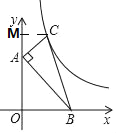
∵A（0，4）、B（4，0），
∴OA=4，OB=4，
∵∠ABO+∠OAB=90°，∠OAB+∠CAM=90°，
∴∠ABO=∠CAM，
∵∠AOB=∠AMC，
∴△ABO∽△CAM，
∴
，
∵AB=2AC，OA=4，OB=4，
∴OA=2，OB=2，
∴C（2，6），
∵C（2，6）在y=
上，
∴k=4，
∴y=
，
当y=4时，x=3，
∵将△ABC沿x轴正方向向右平移m个单位长度，使点A恰好落在双曲线上，
∴m=3，
故选C．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC是边长为3的等边三角形，P是AB边上的一个动点，由A向B运动（P不与A、B重合），Q是BC延长线上一动点，与点P同时以相同的速度由C向BC延长线方向运动（Q不与C重合），
（1）当∠BPQ＝90°时，求AP的长；
（2）过P作PE⊥AC于点E，连结PQ交AC于D，在点P、Q的运动过程中，线段DE的长是否发生变化？若不变，求出DE的长度；若变化，求出变化范围．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如果一个三角形能被一条线段分割成两个等腰三角形，那么称这条线段为这个三角形的特异线，称这个三角形为特异三角形．
（1）如图1，△ABC是等腰锐角三角形，AB=AC(
)，若∠ABC的角平分线BD交AC于点D，且BD是△ABC的一条特异线，则∠BDC=______度；（2）如图2，△ABC中，∠B=2∠C，线段AC的垂直平分线交AC于点D，交BC于点E．求证：AE是△ABC的一条特异线；
（3）如图3，已知△ABC是特异三角形，且∠A=30°，∠B为钝角，求出所有可能的∠B的度数（如有需要，可在答题卡相应位置另外画图）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，进行如下操作：①分别以点A和点C为圆心，以大于
的长为半径作弧，两弧分别相交于点M，N；②作直线MN，交线段AC于点D；③连接BD．则下列结论正确的是( )
A.BD平分∠ABCB.BD⊥ACC.AD=CDD.△ABD≌△CBD
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点O是△ABC角平分线的交点，过点O作MN∥BC分别与AB，AC相交于点M，N，若
，
，
，则△AMN的周长为__________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点D，E，F分别在等边三角形ABC的三边上，且DE⊥AB，EF⊥BC，FD⊥AC，过点F作FH⊥AB于H，则
的值为_________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，
，四边形ABCD的顶点A在
的内部，B，C两点在OM上（C在B，O之间），且
，点D在ON上，若当CD⊥OM时，四边形ABCD的周长最小，则此时AD的长度是__________．
相关试题
