搜索
【题目】如图，点O是△ABC角平分线的交点，过点O作MN∥BC分别与AB，AC相交于点M，N，若
，
，
，则△AMN的周长为__________．
参考答案：
【答案】12
【解析】
根据平行线的性质以及角平分线的性质，可得出∠MOB=∠MBO, ∠NOC=∠NCO,进而得出MO=MB,NO=NC, △AMN的周长可以表示为AB+AC，即可解决问题.
解：∵O是△ABC角平分线的交点
∴∠OBC=∠MBO, ∠OCB=∠NCO
∵MN∥BC
∴∠MOB=∠OBC, ∠NOC=∠OCB
∴∠MOB=∠MBO, ∠NOC=∠NCO,
∴MO=MB,NO=NC,
∵△AMN的周长=AN+AM+MN= AN+AM+MB+NC=AB+AC
又∵
，
，
∴△AMN的周长=5+7=12
故答案为12.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如果一个三角形能被一条线段分割成两个等腰三角形，那么称这条线段为这个三角形的特异线，称这个三角形为特异三角形．
（1）如图1，△ABC是等腰锐角三角形，AB=AC(
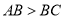)，若∠ABC的角平分线BD交AC于点D，且BD是△ABC的一条特异线，则∠BDC=______度；（2）如图2，△ABC中，∠B=2∠C，线段AC的垂直平分线交AC于点D，交BC于点E．求证：AE是△ABC的一条特异线；
（3）如图3，已知△ABC是特异三角形，且∠A=30°，∠B为钝角，求出所有可能的∠B的度数（如有需要，可在答题卡相应位置另外画图）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，进行如下操作：①分别以点A和点C为圆心，以大于
的长为半径作弧，两弧分别相交于点M，N；②作直线MN，交线段AC于点D；③连接BD．则下列结论正确的是( )
A.BD平分∠ABCB.BD⊥ACC.AD=CDD.△ABD≌△CBD
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，点A、B的坐标分别为（0，4）、（4，0），点C在第一象限内，∠BAC=90°，AB=2AC，函数y=
（x＞0）的图象经过点C，将△ABC沿x轴的正方向向右平移m个单位长度，使点A恰好落在函数y=（x＞0）的图象上，则m的值为（ ）
A.
B. 
C. 3 D.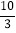 
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点D，E，F分别在等边三角形ABC的三边上，且DE⊥AB，EF⊥BC，FD⊥AC，过点F作FH⊥AB于H，则
的值为_________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，
，四边形ABCD的顶点A在
的内部，B，C两点在OM上（C在B，O之间），且
，点D在ON上，若当CD⊥OM时，四边形ABCD的周长最小，则此时AD的长度是__________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，矩形OABC的顶点A在y轴的正半轴上，点C在x轴的正半轴上，反比例函数y=
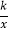（k≠0）的图象的一个分支与AB交于点D，与BC交于点E，DF⊥x轴于点F，EG⊥y轴于点G，交DF于点H．若矩形OGHF和矩形HDBE的面积分别是2和5，则k的值是（ ）
A. 7 B.
C. 2+
D. 10
相关试题
