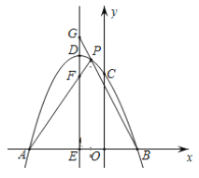
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴相交于
轴相交于![]() 、
、![]() 两点(
两点(![]() 在
在![]() 的左侧),与
的左侧),与![]() 轴相交于点C(0,3),且
轴相交于点C(0,3),且![]() ,
,![]() ,抛物线的顶点为
,抛物线的顶点为![]() .
.
(1)求![]() 、
、![]() 两点的坐标.
两点的坐标.
(2)求抛物线的表达式.
(3)过点![]() 作直线
作直线![]() 轴,交
轴,交![]() 轴于点
轴于点![]() ,点
,点![]() 是抛物线上
是抛物线上![]() ,
,![]() 两点间的一个动点(点
两点间的一个动点(点![]() 不与
不与![]() 、
、![]() 两点重合),
两点重合),![]() 、
、![]() 与直线
与直线![]() 分别相交于点
分别相交于点![]() 、
、![]() 当点
当点![]() 运动时,
运动时,![]() 是否为定值?若是,试求出该定值;若不是,请说明理由.
是否为定值?若是,试求出该定值;若不是,请说明理由.
参考答案:
【答案】(1)A(-3,0) B(1,0);(2)![]() ;(3)是,8
;(3)是,8
【解析】
(1)根据![]() ,
,![]() 的长,可得答案;
的长,可得答案;
(2)根据待定系数法,可得函数解析式;
(3)根据相似三角形的判定与性质,可得![]() ,
,![]() 的长,根据整式的加减,可得答案.
的长,根据整式的加减,可得答案.
解:(1)由抛物线![]() 交
交![]() 轴于
轴于![]() 、
、![]() 两点
两点![]() 在
在![]() 的左侧),且
的左侧),且![]() ,
,![]() ,得
,得![]() 点坐标
点坐标![]() ,
,![]() 点坐标
点坐标![]() ;
;
(2)设抛物线的解析式为![]() ,
,
把![]() 点坐标代入函数解析式,得
点坐标代入函数解析式,得
![]() ,
,
解得![]() ,
,
抛物线的解析式为![]() ;
;
(3)![]() (或
(或![]() 是定值),理由如下:
是定值),理由如下:
过点![]() 作
作![]() 轴交
轴交![]() 轴于
轴于![]() ,如图.
,如图.
设![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ;
;
又![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂对一批灯泡的质量进行随机抽查,见下表:
抽取灯泡数
40
100
150
500
1000
1500
优等品数

36
92
145
474
950
1427
优等品频率
(1)计算表中的优等品的频率(精确到0.001)
(2)根据抽査的灯泡优等品的频率,估计这批灯泡优等品的概率(精确到0.01)
-
科目: 来源: 题型:
查看答案和解析>>【题目】建造一个面积为130m2的长方形养鸡场,鸡场的一边靠墙,墙长为a米,另三边用竹篱笆围成,如果篱笆总长为33米.
(1)求养鸡场的长与宽各为多少米?
(2)若10≤a<18,题中的解的情况如何?
-
科目: 来源: 题型:
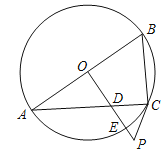
查看答案和解析>>【题目】如图,已知AB是⊙O的直径,过O点作OP⊥AB,交弦AC于点D,交⊙O于点E,且使∠PCA=∠ABC.
(1)求证:PC是⊙O的切线;
(2)若∠P=60°,PC=2,求PE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在矩形ABCD中,动点P从点B出发,沿BC﹣CD﹣DA运动至点A停止.设点P运动的路程为x,△ABP的面积为y,若y关于x的函数图象如图2所示,则y的最大值是( )
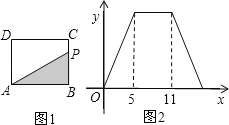
A.55B.30C.16D.15
-
科目: 来源: 题型:
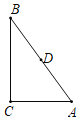
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,点D是AB的中点,点P是直线BC上一点,将△BDP沿DP所在的直线翻折后,点B落在B1处,若B1D⊥BC,则点P与点B之间的距离为( )
A.1B.
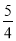 C.1或 3D.
C.1或 3D.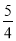 或5
或5 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线y=﹣x+7a+1与直线y=2x﹣2a+4同时经过点P,点Q是以M(0,﹣1)为圆心,MO为半径的圆上的一个动点,则线段PQ的最小值为( )
A.
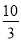 B.
B.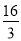 C.
C.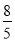 D.
D.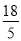
相关试题

