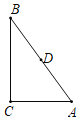
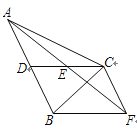
【题目】如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,点D是AB的中点,点P是直线BC上一点,将△BDP沿DP所在的直线翻折后,点B落在B1处,若B1D⊥BC,则点P与点B之间的距离为( )
A.1B.![]() C.1或 3D.
C.1或 3D.![]() 或5
或5
参考答案:
【答案】D
【解析】
分点B1在BC左侧,点B1在BC右侧两种情况讨论,由勾股定理可AB=5,由平行线分线段成比例可得![]() ,可求BE,DE的长,由勾股定理可求PB的长.
,可求BE,DE的长,由勾股定理可求PB的长.
解:如图,若点B1在BC左侧,
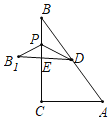
∵∠C=90°,AC=3,BC=4,
∴AB=![]()
∵点D是AB的中点,
∴BD=![]() BA=
BA=![]()
∵B1D⊥BC,∠C=90°
∴B1D∥AC
∴![]()
∴BE=EC=![]() BC=2,DE=
BC=2,DE=![]() AC=
AC=![]()
∵折叠
∴B1D=BD=![]() ,B1P=BP
,B1P=BP
∴B1E=B1D-DE=1
∴在Rt△B1PE中,B1P2=B1E2+PE2,
∴BP2=1+(2-BP)2,
∴BP=![]()
如图,若点B1在BC右侧,
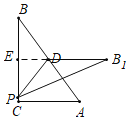
∵B1E=DE+B1D=![]() +
+![]() ,
,
∴B1E=4
在Rt△EB1P中,B1P2=B1E2+EP2,
∴BP2=16+(BP-2)2,
∴BP=5
故选:D.
-
科目: 来源: 题型:
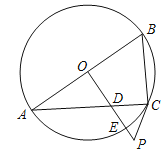
查看答案和解析>>【题目】如图,已知AB是⊙O的直径,过O点作OP⊥AB,交弦AC于点D,交⊙O于点E,且使∠PCA=∠ABC.
(1)求证:PC是⊙O的切线;
(2)若∠P=60°,PC=2,求PE的长.
-
科目: 来源: 题型:
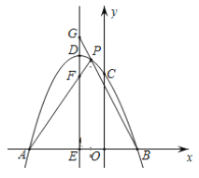
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线
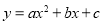 与
与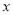 轴相交于
轴相交于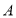 、
、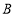 两点(
两点(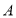 在
在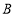 的左侧),与
的左侧),与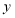 轴相交于点C(0,3),且
轴相交于点C(0,3),且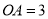 ,
,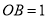 ,抛物线的顶点为
,抛物线的顶点为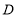 .
. 
(1)求
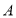 、
、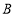 两点的坐标.
两点的坐标.(2)求抛物线的表达式.
(3)过点
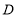 作直线
作直线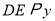 轴,交
轴,交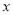 轴于点
轴于点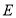 ,点
,点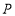 是抛物线上
是抛物线上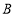 ,
,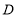 两点间的一个动点(点
两点间的一个动点(点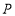 不与
不与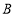 、
、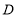 两点重合),
两点重合),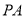 、
、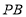 与直线
与直线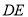 分别相交于点
分别相交于点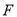 、
、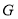 当点
当点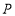 运动时,
运动时,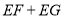 是否为定值?若是,试求出该定值;若不是,请说明理由.
是否为定值?若是,试求出该定值;若不是,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在矩形ABCD中,动点P从点B出发,沿BC﹣CD﹣DA运动至点A停止.设点P运动的路程为x,△ABP的面积为y,若y关于x的函数图象如图2所示,则y的最大值是( )
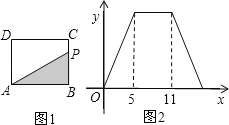
A.55B.30C.16D.15
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线y=﹣x+7a+1与直线y=2x﹣2a+4同时经过点P,点Q是以M(0,﹣1)为圆心,MO为半径的圆上的一个动点,则线段PQ的最小值为( )
A.
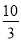 B.
B.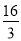 C.
C.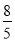 D.
D.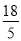
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
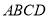 的项点都在坐标轴上,若
的项点都在坐标轴上,若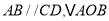 与
与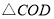 面积分别为
面积分别为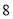 和
和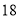 ,若双曲线
,若双曲线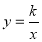 恰好经过
恰好经过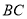 的中点
的中点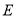 ,则
,则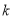 的值为__________.
的值为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,CD是AB边上的中线,E是CD的中点,过点C作AB的平行线交AE的延长线于点F,连接BF.
(1) 求证:CF=AD;
(2) 若CA=CB,∠ACB=90°,试判断四边形CDBF的形状,并说明理由.
相关试题

