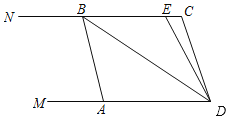
【题目】如图,已知两条直线DM∥CN,线段AB的两个端点A、B分别在直线OM、CN上,∠C=∠BAD,点E在线段BC上,且DB平分∠ADE.
(1)求证:AB∥CD;
(2)若沿着NC方向平移线段AB,那么∠CBD与∠CED度数之间的关系是否随着AB位置的变化而变化?若变化,请找出变化规律;若不变化,请确定它们之间的数量关系.
参考答案:
【答案】(1)见解析;(2)没有变化,∠CDB=![]() ∠CED,见解析
∠CED,见解析
【解析】
(1)欲证明AB∥CD,只要证明∠C=∠NBA即可.
(2)没有变化.利用平行线的性质以及角平分线的定义证明∠CDB=![]() ∠CED即可.
∠CED即可.
解:(1)∵DM∥CN,
∴∠BAD=∠NBA,
∵∠C=∠BAD,
∴∠C=∠NBA,
∴AB∥CD.
(2)结论:没有变化,∠CDB=![]() ∠CED.
∠CED.
理由:∵DB平分∠ADE,
∴∠ADB=∠EDB,
∵DM∥CN,
∴∠ADB=∠CBD,
∴∠CBD=∠EDB,
∵DM∥CN,
∴∠CED=∠EDA,
∵∠EDA=2∠EDB,
∴∠CDB=![]() ∠CED.
∠CED.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点O(0,0),B(1,2).
(1)若点A在y轴上,且三角形AOB的面积为2,求点A的坐标;
(2)若点C的坐标为(3,0),BD∥OC,且BD=OC,求点D的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,已知抛物线y=ax2+bx+c的图像经过点A(0,3)、B(1,0),其对称轴为直线l:x=2,过点A作AC∥x轴交抛物线于点C,∠AOB的平分线交线段AC于点E,点P是抛物线上的一个动点,设其横坐标为m.

(1)求抛物线的解析式;
(2)若动点P在直线OE下方的抛物线上,连结PE、PO,当m为何值时,四边形AOPE面积最大,并求出其最大值;
(3)如图②,F是抛物线的对称轴l上的一点,在抛物线上是否存在点P使△POF成为以点P为直角顶点的等腰直角三角形?若存在,直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题与它的逆命题都为真命题的是( )
A. 已知非零实数x,如果
 为分式,那么它的倒数也是分式。
为分式,那么它的倒数也是分式。B. 如果x的相反数为7,那么x为-7。
C. 如果一个数能被8整除,那么这个数也能被4整除。
D. 如果两个数的和是偶数,那么它们都是偶数。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,自左向右,水平摆放一组小球,按照以下规律排列,如:红球,黄球,绿球,红球,黄球,绿球,…嘉琪依次在小球上标上数字1,2,3,4,5,6,…,则从左往右第100个黄球上所标的数字为__________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】家家乐超市购进一批面粉,标准质量为50千克,现抽取20袋面粉进行称重检测,为记录的方便用
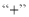 ,表示超过标准的重量,用
,表示超过标准的重量,用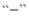 表示不足标准的重量,结果如下表(单位:千克)
表示不足标准的重量,结果如下表(单位:千克) 与标准差(千克)
-2
-1.5
-1
-0.5
0
0.5
1
1.5
袋数
3
2
3
4
1
2
1
4
(1)求这20袋面粉超出或不足的质量为多少?
(2)这20袋面粉平均每袋多少千克?
-
科目: 来源: 题型:
查看答案和解析>>【题目】出租车司机王师傅某天早上营运时是在东西走向的大街上进行的,如果规定向东为正,向西为负,他这天早上所接六位乘客的行车里程(
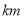 )如下:
)如下: 2,+5,-4,+1,-6,-2
(1)将最后一位乘客送到目的地时,王师傅在早上出发点的什么位置?
(2)若汽车耗油量为
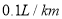 ,这天早上王师傅接送乘客,出租车共耗油多少升?
,这天早上王师傅接送乘客,出租车共耗油多少升?(3)若出租车起步价为6元,起步里程为
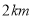 (包括
(包括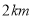 ),超过部分(不足
),超过部分(不足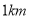 按
按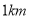 计算)每千米1.5元,王师傅这天早上共得车费多少元?
计算)每千米1.5元,王师傅这天早上共得车费多少元?
相关试题

