【题目】如图①,已知抛物线y=ax2+bx+c的图像经过点A(0,3)、B(1,0),其对称轴为直线l:x=2,过点A作AC∥x轴交抛物线于点C,∠AOB的平分线交线段AC于点E,点P是抛物线上的一个动点,设其横坐标为m.

(1)求抛物线的解析式;
(2)若动点P在直线OE下方的抛物线上,连结PE、PO,当m为何值时,四边形AOPE面积最大,并求出其最大值;
(3)如图②,F是抛物线的对称轴l上的一点,在抛物线上是否存在点P使△POF成为以点P为直角顶点的等腰直角三角形?若存在,直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)y=x2-4x+3.(2)当m=![]() 时,四边形AOPE面积最大,最大值为
时,四边形AOPE面积最大,最大值为![]() .(3)P点的坐标为 :P1(
.(3)P点的坐标为 :P1(![]() ,
,![]() ),P2(
),P2(![]() ,
,![]() ),P3(
),P3(![]() ,
,![]() ),P4(
),P4(![]() ,
,![]() ).
).
【解析】
(1)利用对称性可得点D的坐标,利用交点式可得抛物线的解析式;
(2)设P(m,m2-4m+3),根据OE的解析式表示点G的坐标,表示PG的长,根据面积和可得四边形AOPE的面积,利用配方法可得其最大值;
(3)存在四种情况:
如图3,作辅助线,构建全等三角形,证明△OMP≌△PNF,根据OM=PN列方程可得点P的坐标;同理可得其他图形中点P的坐标.
(1)如图1,设抛物线与x轴的另一个交点为D,
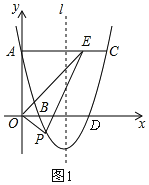
由对称性得:D(3,0),
设抛物线的解析式为:y=a(x-1)(x-3),
把A(0,3)代入得:3=3a,
a=1,
∴抛物线的解析式;y=x2-4x+3;
(2)如图2,设P(m,m2-4m+3),
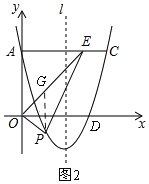
∵OE平分∠AOB,∠AOB=90°,
∴∠AOE=45°,
∴△AOE是等腰直角三角形,
∴AE=OA=3,
∴E(3,3),
易得OE的解析式为:y=x,
过P作PG∥y轴,交OE于点G,
∴G(m,m),
∴PG=m-(m2-4m+3)=-m2+5m-3,
∴S四边形AOPE=S△AOE+S△POE,
=![]() ×3×3+
×3×3+![]() PGAE,
PGAE,
=![]() +
+![]() ×3×(-m2+5m-3),
×3×(-m2+5m-3),
=-![]() m2+
m2+![]() m,
m,
=![]() (m-
(m-![]() ,
,
∵-![]() <0,
<0,
∴当m=![]() 时,S有最大值是
时,S有最大值是![]() ;
;
(3)如图3,过P作MN⊥y轴,交y轴于M,交l于N,
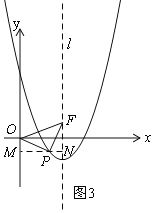
∵△OPF是等腰直角三角形,且OP=PF,
易得△OMP≌△PNF,
∴OM=PN,
∵P(m,m2-4m+3),
则-m2+4m-3=2-m,
解得:m=![]() 或
或![]() ,
,
∴P的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() );
);
如图4,过P作MN⊥x轴于N,过F作FM⊥MN于M,
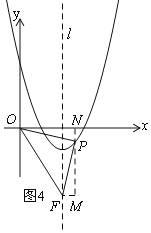
同理得△ONP≌△PMF,
∴PN=FM,
则-m2+4m-3=m-2,
解得:x=![]() 或
或![]() ;
;
P的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() );
);
综上所述,点P的坐标是:(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在四边形ABCD中,AC⊥BD于点E,AB=AC=BD,点M为BC中点,N为线段AM上的点,且MB=MN.
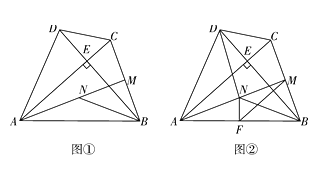
(1)求证:BN平分∠ABE;
(2)若BD=1,连结DN,当四边形DNBC为平行四边形时,求线段BC的长;
(3)如图②,若点F为AB的中点,连结FN、FM,求证:△MFN∽△BDC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点O(0,0),B(1,2).
(1)若点A在y轴上,且三角形AOB的面积为2,求点A的坐标;
(2)若点C的坐标为(3,0),BD∥OC,且BD=OC,求点D的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题与它的逆命题都为真命题的是( )
A. 已知非零实数x,如果
 为分式,那么它的倒数也是分式。
为分式,那么它的倒数也是分式。B. 如果x的相反数为7,那么x为-7。
C. 如果一个数能被8整除,那么这个数也能被4整除。
D. 如果两个数的和是偶数,那么它们都是偶数。
-
科目: 来源: 题型:
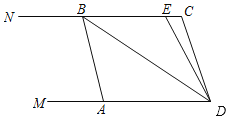
查看答案和解析>>【题目】如图,已知两条直线DM∥CN,线段AB的两个端点A、B分别在直线OM、CN上,∠C=∠BAD,点E在线段BC上,且DB平分∠ADE.
(1)求证:AB∥CD;
(2)若沿着NC方向平移线段AB,那么∠CBD与∠CED度数之间的关系是否随着AB位置的变化而变化?若变化,请找出变化规律;若不变化,请确定它们之间的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,自左向右,水平摆放一组小球,按照以下规律排列,如:红球,黄球,绿球,红球,黄球,绿球,…嘉琪依次在小球上标上数字1,2,3,4,5,6,…,则从左往右第100个黄球上所标的数字为__________.

相关试题

