【题目】用小立方块搭一几何体,它的主视图和俯视图如图所示,这个几何体最少要a个立方块,最多要b个立方块.

(1)求a,b的值
(2)若有理数x,y满足![]() ,
,![]() ,且xy<0,求x+y的值.
,且xy<0,求x+y的值.
参考答案:
【答案】(1)a=10,b=14;(2)4或4
【解析】
(1)由几何体的主视图和俯视图可知,该几何体的主视图第一列3个正方形中每个正方形所在位置最多均可有2个立方块,最少一个正方体所在位置有2个立方块,其余2个所在位置各有1个立方块;主视图第二列1个正方形所在位置只能有2个立方块;主视图第三列每个正方形所在位置最多均可有3个立方块,最少一个正方体所在位置有3个立方块,另外一个所在位置有1个立方块;
(2)将(1)中求得的答案代入条件,根据有理数的乘法运算法则和绝对值的性质判断出x、y的值,然后相加即可得结果.
解:(1)由主视图和俯视图可知:
这样的几何体最少需要(2+1+1)+2+(3+1)=10(个)立方块;
最多需要:2×3+2+3×2=14(个)立方块;
所以a=10,b=14;
(2)由(1)可得![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
因为xy<0,即x、y的符号相反,
当![]() ,则
,则![]() ,此时x+y=1014=4,
,此时x+y=1014=4,
当![]() ,则
,则![]() ,此时x+y=10+14=4,
,此时x+y=10+14=4,
所以x+y的值为4或4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,如果一个点的纵坐标等于横坐标的2倍,那么这个点叫做倍点.例如:点(1,2)是倍点。
(1)已知第一象限内的点A到x轴的距离是1,若点A是倍点,则点A的坐标为________
(2)求反比例函数
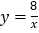 图像上的所有倍点;
图像上的所有倍点;(3)请分析一次函数
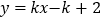 (
(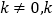 为常数)图像上倍点的情况.
为常数)图像上倍点的情况. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=AC,AE=AF,BE与CF交于点D,则对于下列结论:①△ABE≌△ACF;②△BDF≌△CDE;③D在∠BAC的平分线上.其中正确的是( )
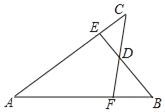
A. ① B. ② C. ①和② D. ①②③
-
科目: 来源: 题型:
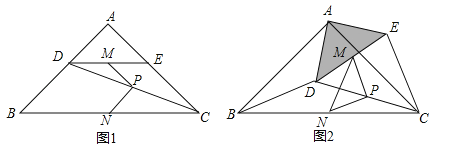
查看答案和解析>>【题目】如图1,在Rt△ABC中,∠A=90°,AB=AC,点D,E分别在边AB,AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点.
(1)观察猜想
图1中,线段PM与PN的数量关系是 ,位置关系是 ;
(2)探究证明
把△ADE绕点A逆时针方向旋转到图2的位置,连接MN,BD,CE,判断△PMN的形状,并说明理由;
(3)拓展延伸
把△ADE绕点A在平面内自由旋转,若AD=4,AB=10,请直接写出△PMN面积的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=
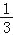 x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P时直线AC下方抛物线上的动点.
x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P时直线AC下方抛物线上的动点.
(1)求抛物线的解析式;(2)过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标;
(3)当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,若存在,求出点Q的坐标,若不存在,请说明理由.
-
科目: 来源: 题型:
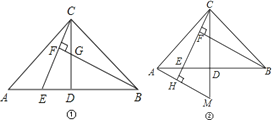
查看答案和解析>>【题目】已知:在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点.
(1)直线BF垂直于直线CE于点F,交CD于点G(如图①),求证:AE=CG;
(2)直线AH垂直于直线CE,垂足为点 H,交CD的延长线于点M(如图②),
求证:CM=BE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,数轴上有两点A、B对应的数分别为1,5,点P为数轴上一动点,其对应的数为x.
(1)若点P到点A、B的距离相等,求点A、B的距离及x的值.
(2)数轴上是否存在点P,使得点P到点A、B的距离之和最小?若存在,请求出最小值;并求出取得最小值时x可以取的整数值;若不存在,说明理由.
(3)点A、B分别以3个单位长度/秒,2个单位长度/秒的速度向右运动,同时点P以4个单位长度/秒的速度从O点向左运动,当遇到A时,点P立即以不变的速度向右运动,当遇到B时,点P立即以不变的速度向左运动,并不停往返于点A与点B之间,求当点A与点B重合时,点P所经过的总路程是多少?
相关试题

