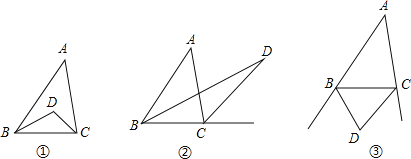
【题目】如图①,△ABC中,DC,BD分别是∠ACB和∠ABC的平分线,且∠A=α
(1)用含α的代数式表示∠CDB;
(2)若把图①中∠ACB的平分线DC改为∠ACB的外角的平分线(如图②),怎样用含α的代数式表示∠CDB.
(3)若把图①中“DC,DB分别是∠ACB和∠ABC的平分线”改成“DC,BD分别是∠ACB和∠ABC的外角的平分线”,(如图③),怎样用含α的代数式表示∠CDB.
参考答案:
【答案】(1)90°+![]() ;(2)
;(2)![]() ;(3)90°-
;(3)90°-![]() ;
;
【解析】
(1)利用三角形的内角和定理,及角平分线定义;
(2)利用三角形的外角等于和它不相邻的两个内角的和求解;
(3)利用三角形的内角和定理,及角平分线定义,邻补角定义.
(1)∵∠A=α,
∴∠ABC+∠ACB=180°﹣α,
∵DC,BD分别是∠ACB和∠ABC的平分线,
∴∠DBC+∠DCB=![]() ×(∠ABC+∠ACB)=90°﹣
×(∠ABC+∠ACB)=90°﹣![]() α,
α,
∴∠CDB=180°﹣(∠DBC+∠DCB)=90°+![]() ;
;
(2)设BC的延长线上有一点E.
∵∠DCE是△BCD的一个外角,
∴∠D=∠DCE﹣∠DBC,
同理:∠A=∠ACE﹣∠ABC,
∵CD和BD分别为角平分线,
∴∠DCE=![]() ∠ACE,∠DBC=
∠ACE,∠DBC=![]() ∠ABC,
∠ABC,
∴∠CDB=![]() ;
;
(3)∵∠A=α,
∴∠ABC+∠ACB=180°﹣α,
∵DC,BD分别是∠ACB和∠ABC的外角的平分线,
∴∠DBC+∠DCB=![]() ×[360°﹣(∠ABC+∠ACB)]=90°+
×[360°﹣(∠ABC+∠ACB)]=90°+![]() ,
,
∴∠CDB=CDB=180°﹣(∠DBC+∠DCB)=90°﹣![]() .
.
-
科目: 来源: 题型:
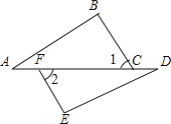
查看答案和解析>>【题目】如图,已知:∠A=∠D,∠1=∠2,下列条件中能使△ABC≌△DEF的有_____.
①∠E=∠B;②ED=BC;③AB=EF;④AF=CD.
-
科目: 来源: 题型:
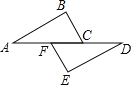
查看答案和解析>>【题目】数学课上,柴老师出了一道题:如图,已知∠A=∠D,∠BCA=∠EFD.要使△ABC≌△DEF,你还应给出的条件是什么?下面四个同学做了回答:小马:“增加∠E=∠B;小李:“增加ED=BA;”小周:“增加AB=EF;”小胡:“增加AF=DC.”针对上面四个同学的回答,你认为正确的是_____.(填上你认为正确的同学的名字)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰三角形ABC中,一腰AC上的中线BD将三角形的周长分成9cm和15cm两部分,求这个三角形的腰长和底边的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】八年级(3)班共有学生54人,学习委员调查了班级学生参加课外活动的情况(每人只参加一项活动),其中:参加读书活动的18人,参加科技活动的人数占全班总人数的
 ,参加艺术活动的比参加科技活动的多3人,所调查班级同学参加体育活动情况如图所示,则在扇形图中表示参加体育活动人数的扇形的圆心角大小为( )
,参加艺术活动的比参加科技活动的多3人,所调查班级同学参加体育活动情况如图所示,则在扇形图中表示参加体育活动人数的扇形的圆心角大小为( )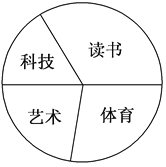
A. 100° B. 110°
C. 120° D. 130°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC和△DEC都是等腰直角三角形,C为它们的公共直角顶点,连AD,BE,F为线段AD的中点,连接CF

(1)如图1,当D点在BC上时,求证:①BE=2CF,②BE⊥CF.
(2)如图2,把△DEC绕C点顺时针旋转一个锐角,其他条件不变,问(1)中的关系是否仍然成立?如果成立请证明.如果不成立,请写出相应的正确的结论并加以证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】光明中学八年级甲、乙、丙三个班中,每班的学生人数都为40名,某次数学考试的成绩统计如图:(每组分数含最小值,不含最大值)
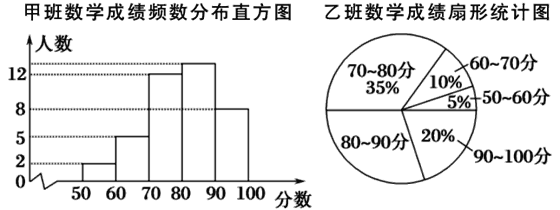
丙班数学成绩频数统计表
分数
50~60
60~70
70~80
80~90
90~100
人数
1
4
15
11
9
根据上图及统计表提供的信息,则80~90分这一组人数最多的班是________
相关试题

