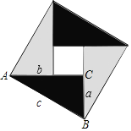
【题目】现用4个全等的直角三角形拼成如图所示“弦图”.Rt△ABC中,∠ACB=90°,若AC=b,BC=a,请你利用这个图形解决下列问题:
(1)试说明a2+b2=c2;
(2)如果大正方形的面积是6,小正方形的面积是2,求(a+b)2的值.
参考答案:
【答案】(1)详见解析;(2)10.
【解析】
(1)根据题意,我们可在图中找等量关系,由中间的小正方形的面积等于大正方形的面积减去四个直角三角形的面积,列出等式化简即可得出勾股定理的表达式.
(2)根据完全平方公式的变形解答即可.
(1)∵大正方形面积为c2,直角三角形面积为![]() ab,小正方形面积为(b-a)2,
ab,小正方形面积为(b-a)2,
∴c2=4×![]() ab+(a-b)2=2ab+a2-2ab+b2即c2=a2+b2.;
ab+(a-b)2=2ab+a2-2ab+b2即c2=a2+b2.;
(2)由图可知,(b-a)2=2,4×![]() ab=6-2=4,∴ab=2,
ab=6-2=4,∴ab=2,
∴(a+b)2=(b-a)2+4ab=2+8=10.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点D在△ABC的边AC上,要判定△ADB与△ABC相似,添加一个条件,不正确的是( )
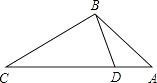
A.∠ABD=∠C
B.∠ADB=∠ABC
C.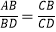
D.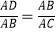
-
科目: 来源: 题型:
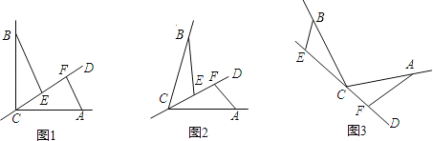
查看答案和解析>>【题目】CD经过∠BCA顶点C的一条直线,CA=CB.E,F分别是直线CD上两点,且∠BEC=∠CFA=∠α.
(1)若直线CD经过∠BCA的内部,且E,F在射线CD上,请解决下面两个问题:
①如图1,若∠BCA=90°,∠α=90°,则BE_____CF;EF_____|BE﹣AF|(填“>”,“<”或“=”);
②如图2,若0°<∠BCA<180°,请添加一个关于∠α与∠BCA关系的条件_____,使①中的两个结论仍然成立。
(2)如图3,若直线CD经过∠BCA的外部,∠α=∠BCA,请提出EF,BE,AF三条线段数量关系的合理猜想并给出理由。.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O是等边△ABC内一点.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.已知∠AOB=110°.

(1)求证:△COD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由;
(3)探究:当α为多少度时,△AOD是等腰三角形.
-
科目: 来源: 题型:
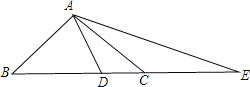
查看答案和解析>>【题目】(1)如图,在在△ABC中,已知∠BAC=900,AB=AC,点D在BC上,且BD=BA,点E在BC的延长线上,CE=CA,求∠DAE的度数;
(2)如果把(1)中的“AB=AC”条件去掉,其余条件不变,那么∠DAE的度数改变吗?为什么?
(3)如果把(1)中的“∠BAC=900”改成“∠BAC>900”其余条件不变,试探究∠DAE与∠BAC的数量关系式,试证明.
-
科目: 来源: 题型:
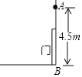
查看答案和解析>>【题目】如图,有一个由传感器A控制的灯,要装在门上方离地面4.5m的墙上,任何东西只要移至该灯5m及5m内,灯就会自动发光,小明身高1.5m,他走到离墙_______的地方灯刚好发光.
-
科目: 来源: 题型:
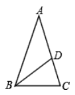
查看答案和解析>>【题目】如图,在等腰三角形ABC中,AB=AC,点D为AC上一点,且AD=BD=BC,则等腰三角形ABC的顶角度数为__________________.
相关试题

