【题目】如图,四边形ABCD为矩形,F为对角线BD上一点,点E在BA延长线上.
(1)如图①,若F为矩形对角线AC、BD的交点,点E在BA延长线上且BE=AC,连接DE,M是DE的中点,连接BM,FM若AD=6,FM=![]() ,求线段AE的长;
,求线段AE的长;
(2)如图②,过点F作FE⊥BD交AD于点H,交BA延长线于点E,连接AF,当FD=FE时,求证:HA+AB=![]() AF.
AF.

参考答案:
【答案】(1)3;(2)见解析
【解析】
(1)由矩形的性质可得AC=BD,BF=DF,由中位线定理可得BE=2MF,再由勾股定理可求AB的长,即可求AE的长;
(2)如图②,过点F作FN⊥AF交AB的延长线于点N,由“ASA”可证△EFN≌△DFA,可得∠DAF=∠N,AF=FN,由等腰直角三角形的性质可得AN=![]() ,由“ASA”可证△AHF≌△NBF,可证AH=BN,即可得结论.
,由“ASA”可证△AHF≌△NBF,可证AH=BN,即可得结论.
(1)∵四边形ABCD是矩形
∴AC=BD,BF=DF,
∵M是DE的中点,BF=DF,
∴BE=2MF=![]() ,
,
∵BE=AC,AC=BD
∴BD=![]() ,
,
∴AB=![]() ,
,
∴AE=BE﹣AB=3,
(2)如图②,过点F作FN⊥AF交AB的延长线于点N,

∵EF⊥DF,EA⊥AD,
∴∠E+∠AHE=90°,∠ADF+∠DHF=90°,
∴∠E=∠ADF,
∵∠AFN=∠EFD=90°,
∴∠AFD=∠EFN,且∠E=∠ADF,且EF=DF,
∴△EFN≌△DFA(ASA)
∴∠DAF=∠N,AF=FN,且∠AFN=90°,
∴AN=![]() AF,
AF,
∵∠AFN=∠EFB=90°,
∴∠AFH=∠BFN,且∠DAF=∠N,AF=FN,
∴△AHF≌△NBF(ASA),
∴AH=BN(全等三角形对应边相等),
∵AN=![]() AF,
AF,
∴AB+BN=AB+AH=![]() AF,
AF,
-
科目: 来源: 题型:
查看答案和解析>>【题目】在某一电路中,保持电压不变,电流 I(安培)和电阻 R(欧姆)成反比例,当电阻 R=5欧姆时,电流 I=2安培.
(1)求 I与 R之间的函数关系式;
(2)当电流 I=0.5时,求电阻 R的值;
(3)若电阻的最大值为欧姆20,请你写出电流的范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y1=﹣
 x2+bx+c的图象与x轴、y轴分别交于点A(﹣1,0)和点B(0,2),图象的对称轴交x轴于点C,一次函数y2=mx+n的图象经过点B、C.
x2+bx+c的图象与x轴、y轴分别交于点A(﹣1,0)和点B(0,2),图象的对称轴交x轴于点C,一次函数y2=mx+n的图象经过点B、C.(1)求二次函数的解析式y1和一次函数的解析式y2;
(2)点P在x轴下方的二次函数图象上,且S△ACP=33,求点P的坐标;
(3)结合图象,求当x取什么范围的值时,有y1≤y2.

-
科目: 来源: 题型:
查看答案和解析>>【题目】春天到了,鲜花盛开,人们都喜欢用美丽的花朵装点家庭,北碚花市生意兴隆,某花店老板三月份购进一批山茶花、绣球花共1000株,进价均为每株42元,山茶花以每株80元、绣球花以每株64元的价格销售.
(1)若要求三月份的总获利至少33200元,问该老板至少应购进山茶花多少株?
(2)四月份绣球花品种丰富、花型饱满,在进价不变的情况下,该老板决定调整价格,将山茶花的价格在三月份的基础上下调a%(降价后售价不低于进价),绣球花的价格上调
 a%,同时山茶花的销量较三月份最低利润时销量下降了
a%,同时山茶花的销量较三月份最低利润时销量下降了 a%,绣球花的销量较月份最低利润时销量上升了40%,结果四月份的销售额比三月份最低利润时增加了3520元,求a的值.
a%,绣球花的销量较月份最低利润时销量上升了40%,结果四月份的销售额比三月份最低利润时增加了3520元,求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
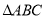 中,
中,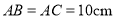 ,
,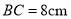 ,点
,点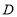 为
为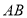 的中点,点
的中点,点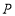 在线段
在线段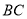 上以
上以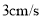 的速度由
的速度由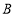 点向
点向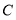 点运动(点
点运动(点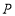 不与点
不与点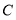 重合),同时点
重合),同时点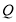 在线段
在线段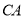 上由
上由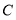 点向
点向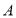 点运动.
点运动.
(1)若点
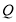 的运动速度与点
的运动速度与点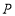 的运动速度相等,当运动时间是
的运动速度相等,当运动时间是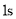 时,
时,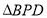 与
与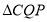 是否全等?请说明理由;
是否全等?请说明理由;(2)若点
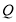 的运动速度与点
的运动速度与点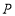 的运动速度不相等,当
的运动速度不相等,当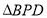 与
与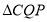 全等时,点
全等时,点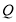 的运动时间是_______________;运动速度是_________________.
的运动时间是_______________;运动速度是_________________. -
科目: 来源: 题型:
查看答案和解析>>【题目】某学校冬季储煤120吨,若每天用煤 x吨,经过 y天可以用完.
(1)请与出 y与 x之间的函数关系式;
(2)画出函数的图象;
(3)当每天的用煤量为1.2~1.5吨时,这些煤可用的天数在什么范围?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在
 和
和 中
中 ,
, ,
, ,连接
,连接 ,
, ,
, 绕点
绕点 自由旋转.
自由旋转.
(1)当
 在
在 边上时,
边上时,①线段
 和线段
和线段 的关系是____________________;
的关系是____________________;②若
 ,则
,则 的度数为____________;
的度数为____________;(2)如图2,点
 不在
不在 边上,
边上, ,
, 相交于点
相交于点 ,(l)问中的线段
,(l)问中的线段 和线段
和线段 的关系是否仍然成立?并说明理由.
的关系是否仍然成立?并说明理由.
相关试题

