【题目】如图①有一个宝塔,它的地基边缘是周长为26m的正五边形ABCDE(如图②),点O为中心.(下列各题结果精确到0.1m)
(1)求地基的中心到边缘的距离;
(2)己知塔的墙体宽为1m,现要在塔的底层中心建一圆形底座的塑像,并且留出最窄处为1.6m的观光通道,问塑像底座的半径最大是多少?

参考答案:
【答案】(1)3.6m;(2)1m.
【解析】试题分析:(1)构造一个由正多边形的边心距、半边和半径组成的直角三角形.根据正五边形的性质得到半边所对的角是![]() =36°,再根据题意中的周长求得该正五边形的半边是26÷10=2.6,最后由该角的正切值进行求解;
=36°,再根据题意中的周长求得该正五边形的半边是26÷10=2.6,最后由该角的正切值进行求解;
(2)根据(1)中的结论、塔的墙体宽为1m和最窄处为1.6m的观光通道,进行计算.
试题解析:(1)作OM⊥AB于点M,连接OA、OB,则OM为边心距,∠AOB是中心角.
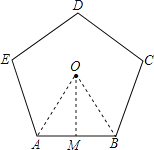
由正五边形性质得∠AOB=360°÷5=72°.
又AB=![]() ×26=5.2,
×26=5.2,
∴AM=2.6,∠AOM=36°,
在Rt△AMO中,边心距OM=![]()
(2)3.6-1-1.6=1(m).
答:地基的中心到边缘的距离约为3.6m,塑像底座的半径最大约为1m.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,△DEF是由△ABC绕点O顺时针旋转180°后形成的图形;
(1)请你指出图中所有相等的线段;
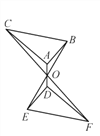
(2)图中哪些三角形可以被看成是关于点O成中心对称关系?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4,…均为等边三角形,若OA1=2,则△A5B5A6的边长为( )

A. 8 B. 16 C. 24 D. 32
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠B=10°,∠ACB=20°,AB=4cm,△ABC逆时针旋转一定角度后与△ADE重合,且点C恰好成为AD的中点.
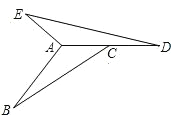
(1)指出旋转中心,并求出旋转的度数;
(2)求出∠BAE的度数和AE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,∠1=∠2,则不一定能使△ABD≌△ACD的条件是 ( )

A. AB=AC B. BD=CD C. ∠B=∠C D. ∠BDA=∠CDA
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,边长为2的正五边形ABCDE内接于⊙O,AB、DC的延长线交于点F,过点E作EG∥CB交BA的延长线于点G.

(1)求证: ;
;
(2)证明:EG与⊙O相切,并求AG、BF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】今年,我省启动了“关爱留守儿童工程”.某村小为了了解各年级留守儿童的数量,对一到六年级留守儿童数量进行了统计,得到每个年级的留守儿童人数分别为10,15,10,17,18,20.对于这组数据,下列说法错误的是( )
A.平均数是15 B.众数是10 C.中位数是17 D.方差是
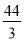
相关试题

