【题目】如图,△ABC中,∠B=10°,∠ACB=20°,AB=4cm,△ABC逆时针旋转一定角度后与△ADE重合,且点C恰好成为AD的中点.
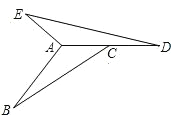
(1)指出旋转中心,并求出旋转的度数;
(2)求出∠BAE的度数和AE的长.
参考答案:
【答案】(1)旋转中心是点A,150°;(2)60°,2.
【解析】
试题分析:(1)根据旋转的性质可知对应点到旋转中心的距离相等以及每一对对应点与旋转中心连线所构成的旋转角相等,所以可求出:∠CAE=BAD=180°-∠B-∠ACB=150°,从而确定旋转中心和旋转角度;
(2)利用周角的定义可求出∠BAE=360°-150°×2=60°,全等的性质可知AE=![]() AB=2cm.
AB=2cm.
试题解析::(1)∵△ABC逆时针旋转一定角度后与△ADE重合,A为顶点,
∴旋转中心是点A;
根据旋转的性质可知:∠CAE=∠BAD=180°-∠B-∠ACB=150°,
∴旋转角度是150°;
(2)由(1)可知:∠BAE=360°-150°×2=60°,
由旋转可知:△ABC≌△ADE,
∴AB=AD,AC=AE,又C为AD中点,
∴AC=AE=![]() AB=
AB=![]() ×4=2cm.
×4=2cm.
考点: 旋转的性质.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB=30°,OP平分∠AOB,PD⊥OB于D,PC∥OB交OA于C,若PC=6,则PD= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,△DEF是由△ABC绕点O顺时针旋转180°后形成的图形;
(1)请你指出图中所有相等的线段;
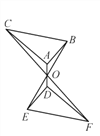
(2)图中哪些三角形可以被看成是关于点O成中心对称关系?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4,…均为等边三角形,若OA1=2,则△A5B5A6的边长为( )

A. 8 B. 16 C. 24 D. 32
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①有一个宝塔,它的地基边缘是周长为26m的正五边形ABCDE(如图②),点O为中心.(下列各题结果精确到0.1m)
(1)求地基的中心到边缘的距离;
(2)己知塔的墙体宽为1m,现要在塔的底层中心建一圆形底座的塑像,并且留出最窄处为1.6m的观光通道,问塑像底座的半径最大是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,∠1=∠2,则不一定能使△ABD≌△ACD的条件是 ( )

A. AB=AC B. BD=CD C. ∠B=∠C D. ∠BDA=∠CDA
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,边长为2的正五边形ABCDE内接于⊙O,AB、DC的延长线交于点F,过点E作EG∥CB交BA的延长线于点G.

(1)求证: ;
;
(2)证明:EG与⊙O相切,并求AG、BF的长.
相关试题

