【题目】已知:如图,边长为2的正五边形ABCDE内接于⊙O,AB、DC的延长线交于点F,过点E作EG∥CB交BA的延长线于点G.

(1)求证: ![]() ;
;
(2)证明:EG与⊙O相切,并求AG、BF的长.
参考答案:
【答案】(1)见解析;(2)见解析
【解析】试题分析:欲证AB2=AGBF,可证△EAG∽△FBC及正五边形ABCDE的特点得出;求AG、BF的长,需连接EF,易证明EF⊥BC,得出EF⊥EG,依据EG与⊙O相切,用切线的性质得出.
试题解析:证明:(1)易证五边形ABCDE的外角∠FCB=∠EAG=∠FBC,
∵EG∥CB,
∴∠EAG=∠FBC.
∴△EAG∽△FBC.
∴![]() ,即BCAE=AGBF.
,即BCAE=AGBF.
又∵BC=AE=AB,
∴![]() .①
.①
(2)连接EF,由(1)可知FB=FC,即△FBC为等腰三角形,易知BA=CD,

∴FA=FD,
∴EF⊥BC且EF平分BC,
∴EF过圆心O.
又∵EG∥CB,∴EF⊥EG,
∴EG与⊙O相切.
∴![]() .
.
由(1)可知∠G=∠EAG,∴EG=EA=2,
设AG=x,则![]() ,解得
,解得![]()
∴AG=![]() ,代入①中可得:BF=
,代入①中可得:BF=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠B=10°,∠ACB=20°,AB=4cm,△ABC逆时针旋转一定角度后与△ADE重合,且点C恰好成为AD的中点.
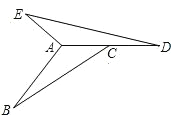
(1)指出旋转中心,并求出旋转的度数;
(2)求出∠BAE的度数和AE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①有一个宝塔,它的地基边缘是周长为26m的正五边形ABCDE(如图②),点O为中心.(下列各题结果精确到0.1m)
(1)求地基的中心到边缘的距离;
(2)己知塔的墙体宽为1m,现要在塔的底层中心建一圆形底座的塑像,并且留出最窄处为1.6m的观光通道,问塑像底座的半径最大是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,∠1=∠2,则不一定能使△ABD≌△ACD的条件是 ( )

A. AB=AC B. BD=CD C. ∠B=∠C D. ∠BDA=∠CDA
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年,我省启动了“关爱留守儿童工程”.某村小为了了解各年级留守儿童的数量,对一到六年级留守儿童数量进行了统计,得到每个年级的留守儿童人数分别为10,15,10,17,18,20.对于这组数据,下列说法错误的是( )
A.平均数是15 B.众数是10 C.中位数是17 D.方差是
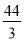
-
科目: 来源: 题型:
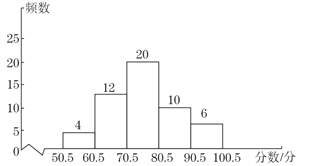
查看答案和解析>>【题目】某校举办以“保护环境,治理雾霾,从我做起”为主题的演讲比赛,现将所有比赛成绩(得分取整数,满分为100分)进行整理后分为5组,并绘制成如图所示的频数直方图.根据频数分布直方图提供的信息,下列结论:①参加比赛的学生共有52人;②比赛成绩为65分的学生有12人;③比赛成绩的中位数落在70.5~80.5分这个分数段;④如果比赛成绩在80分以上(不含80分)可以获得奖励,则本次比赛的获奖率约为30.8%.正确的是________.(把所有正确结论的序号都填在横线上)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是交警在一个路口统计的某个时段来往车辆的车速(单位:km/h).

(1)计算这些车的平均速度.
(2)车速的众数是多少?
(3)车速的中位数是多少?
相关试题

