【题目】化简求值:
(1)当a=﹣1,b=2时,求代数式﹣2(ab﹣3b2)﹣[6b2﹣(ab﹣a2)]的值
(2)先化简,再求值:4xy﹣2(![]() x2﹣3xy+2y2)+3(x2﹣2xy),当(x﹣3)2+|y+1|=0,求式子的值
x2﹣3xy+2y2)+3(x2﹣2xy),当(x﹣3)2+|y+1|=0,求式子的值
(3)若(2mx2﹣x+3)﹣(3x2﹣x﹣4)的结果与x的取值无关,求m的值
参考答案:
【答案】(1)﹣ab﹣a2,1;(2)4xy﹣4y2,﹣16;(3)m=![]() .
.
【解析】
(1)根据去括号、合并同类项,可化简整式,根据代数式求值,可得答案.
(2)原式去括号、合并同类项即可化简,再利用非负数的性质得出x、y的值,继而代入计算可得;
(3)与x无关说明含x的项都被消去,由此可得出m的值.
解:(1)原式=﹣2ab+6b2﹣6b2+ab﹣a2,
=﹣ab﹣a2,
当a=﹣1、b=2时,
原式=﹣(﹣1)×2﹣(﹣1)2,
=2﹣1,
=1;
(2)原式=4xy﹣3x2+6xy﹣4y2+3x2﹣6xy,
=4xy﹣4y2,
∵(x﹣3)2+|y+1|=0,
∴x=3、y=﹣1,
则原式=4×3×(﹣1)﹣4×(﹣1)2,
=﹣12﹣4,
=﹣16;
(3)原式=2mx2﹣x+3﹣3x2+x+4,
=(2m﹣3)x2+7,
∵结果与x的取值无关,
∴2m﹣3=0,
解得:m=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】父亲告诉小明:“距离地面越高,温度越低”,并给小明出示了下面的表格:
距离地面高度(千米)h
0
1
2
3
4
5
温度(℃)t
20
14
8
2
﹣4
﹣10
根据表中,父亲还给小明出了下面几个问题,请你帮助小明回答下列问题:
(1)表中自变量是 ;因变量是 ;当地面上(即h=0时)时,温度是 ℃.
(2)如果用h表示距离地面的高度,用t表示温度,请写出满足t与h关系的式子.
(3)计算出距离地面6千米的高空温度是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c的顶点坐标为(2,9),与y轴交于点A(0,5),与x轴交于点E、B.
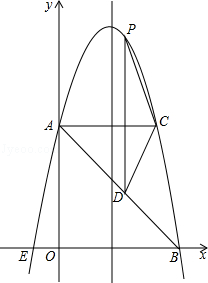
(1)求二次函数y=ax2+bx+c的表达式;
(2)过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一点(点P在AC上方),作PD平行于y轴交AB于点D,问当点P在何位置时,四边形APCD的面积最大?并求出最大面积;
(3)若点M在抛物线上,点N在其对称轴上,使得以A、E、N、M为顶点的四边形是平行四边形,且AE为其一边,求点M、N的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】解方程
(1)4x﹣5=3x+2
(2)
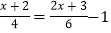
(3)2x﹣3(6﹣x)=3x﹣4(5﹣x)
(4)
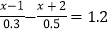
-
科目: 来源: 题型:
查看答案和解析>>【题目】某研究机构经过抽样调查,发现当地1500个老年人的养老模式主要有A,B,C,D,E五种,统计结果如图,那么下列说法不正确的是( )
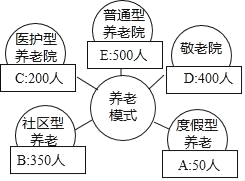
A. 选择A型养老的频率是
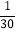
B. 可以估计当地30000个老年人中有8000人选择C型养老
C. 样本容量是1500
D. 总体是当地1500个老年人的养老模式
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在坐标系中放置一菱形OABC,已知∠ABC=60°,OA=1.先将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2014次,点B的落点依次为B1,B2,B3,…,则B2014的坐标为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,∠ABC=90°,AB=BC=2
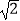 ,E、F分别是AD、CD的中点,连接BE、BF、EF.若四边形ABCD的面积为6,则△BEF的面积为( )
,E、F分别是AD、CD的中点,连接BE、BF、EF.若四边形ABCD的面积为6,则△BEF的面积为( ) 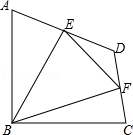
A.2
B.
C.
D.3
相关试题

