【题目】如图,在四边形ABCD中,∠ABC=90°,AB=BC=2 ![]() ,E、F分别是AD、CD的中点,连接BE、BF、EF.若四边形ABCD的面积为6,则△BEF的面积为( )
,E、F分别是AD、CD的中点,连接BE、BF、EF.若四边形ABCD的面积为6,则△BEF的面积为( ) 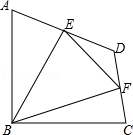
A.2
B.![]()
C.![]()
D.3
参考答案:
【答案】C
【解析】解:连接AC,过B作EF的垂线交AC于点G,交EF于点H, ∵∠ABC=90°,AB=BC=2 ![]() ,
,
∴AC= ![]() =
= ![]() =4,
=4,
∵△ABC为等腰三角形,BH⊥AC,
∴△ABG,△BCG为等腰直角三角形,
∴AG=BG=2
∵S△ABC= ![]() ABAC=
ABAC= ![]() ×2
×2 ![]() ×2
×2 ![]() =4,
=4,
∴S△ADC=2,
∵ ![]() =2,
=2,
∵△DEF~△DAC,
∴GH= ![]() BG=
BG= ![]() ,
,
∴BH= ![]() ,
,
又∵EF= ![]() AC=2,
AC=2,
∴S△BEF= ![]() EFBH=
EFBH= ![]() ×2×
×2× ![]() =
= ![]() ,
,
故选C.
方法二:S△BEF=S四边形ABCD﹣S△ABE﹣S△BCF﹣S△FED ,
易知S△ABE+S△BCF= ![]() S四边形ABCD=3,S△EDF=
S四边形ABCD=3,S△EDF= ![]() ,
,
∴S△BEF=S四边形ABCD﹣S△ABE﹣S△BCF﹣S△FED=6﹣3﹣ ![]() =
= ![]() .
.
故选C.
连接AC,过B作EF的垂线,利用勾股定理可得AC,易得△ABC的面积,可得BG和△ADC的面积,三角形ABC与三角形ACD同底,利用面积比可得它们高的比,而GH又是△ACD以AC为底的高的一半,可得GH,易得BH,由中位线的性质可得EF的长,利用三角形的面积公式可得结果.
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简求值:
(1)当a=﹣1,b=2时,求代数式﹣2(ab﹣3b2)﹣[6b2﹣(ab﹣a2)]的值
(2)先化简,再求值:4xy﹣2(
 x2﹣3xy+2y2)+3(x2﹣2xy),当(x﹣3)2+|y+1|=0,求式子的值
x2﹣3xy+2y2)+3(x2﹣2xy),当(x﹣3)2+|y+1|=0,求式子的值(3)若(2mx2﹣x+3)﹣(3x2﹣x﹣4)的结果与x的取值无关,求m的值
-
科目: 来源: 题型:
查看答案和解析>>【题目】某研究机构经过抽样调查,发现当地1500个老年人的养老模式主要有A,B,C,D,E五种,统计结果如图,那么下列说法不正确的是( )
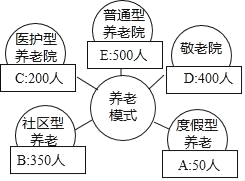
A. 选择A型养老的频率是
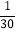
B. 可以估计当地30000个老年人中有8000人选择C型养老
C. 样本容量是1500
D. 总体是当地1500个老年人的养老模式
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在坐标系中放置一菱形OABC,已知∠ABC=60°,OA=1.先将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2014次,点B的落点依次为B1,B2,B3,…,则B2014的坐标为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是菱形,对角线AC,BD相交于点O,DH⊥AB于点H,连接OH,求证:∠DHO=∠DCO.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解食品安全状况,质监部门抽查了甲、乙、丙、丁四个品牌饮料的质量,将收集的数据整理并绘制成图1和图2两幅尚不完整的统计图,请根据图中的信息,完成下列问题:
(1)这次抽查了四个品牌的饮料共 瓶;
(2)请你在答题卡上补全两幅统计图;
(3)若四个品牌饮料的平均合格率是95%,四个品牌饮料月销售量约20万瓶,请你估计这四个品牌的不合格饮料有多少瓶?

-
科目: 来源: 题型:
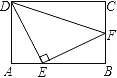
查看答案和解析>>【题目】如图,矩形ABCD中,点E、F分别在AB、BC上,△DEF为等腰直角三角形,∠DEF=90°,AD+CD=10,AE=2,求AD的长.
相关试题

