【题目】如图,四边形ABCD为⊙O的内接四边形,且对角线AC为直径,AD=BC,过点D作DG⊥AC,垂足为E,DG分别与AB及CB延长线交于点F、M.
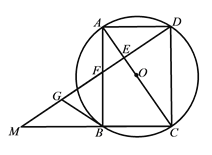
(1)求证:四边形ABCD是矩形;
(2)若点G为MF的中点,求证:BG是⊙O的切线;
(3)若AD=4,CM=9,求四边形ABCD的面积.
参考答案:
【答案】(1)证明见解析;(2)证明见解析; (3)S矩形ABCD=24.
【解析】试题分析:(1)根据AC为 O直径,得到∠ADC=∠CBA=90°,通过全等三角形得到CD=AB,推出四边形ABCD是平行四边形,根据矩形的判定定理得到结论;
(2)根据直角三角形的性质得到NB=![]() MF=NF,根据等腰三角形的性质和余角的性质即可得到NB是 O的切线;
MF=NF,根据等腰三角形的性质和余角的性质即可得到NB是 O的切线;
(3)根据四边形ABCD是矩形,推出△ACD∽△DMC,根据相似三角形的性质列比例式得到![]() ,从而求得DC=6,根据矩形的面积公式即可得到结论.
,从而求得DC=6,根据矩形的面积公式即可得到结论.
试题解析:
(1)证明:∵AC是⊙O的直径,
∴∠ADC=∠ABC=90°.
在Rt△ADC和Rt△CBA中,
AC=CA,AD=CB,

∴Rt△ADC≌Rt△CBA,
∴∠CAD=∠ACB,
∴AD∥BC,又AD=BC,
∴四边形ABCD是平行四边形,又∠ABC=90°,
∴□ABCD是矩形.
(2)证明:连接OB,
在Rt△MBF中,G是MF的中点,
∴BG=![]() MF=FG,
MF=FG,
∴∠GBF=∠GFB=∠AFE.
∵OA=OB,
∴∠OBA=∠OAB.
∵DG⊥AC,
∴∠AFE+∠OAB=90°,
∴∠GBF+∠OBA=90°,
即OB⊥BG,
∴BG是⊙O的切线.
(3)解:由(1)得四边形ABCD是矩形,
∴∠ADC=∠DCM=90°又AC⊥DG,
∴∠CDM+∠ACD=90°,∠CDM+∠M=90°
∴∠ACD=∠M
又∠ADC=∠DCM,
∴△ACD∽△DMC,
∴![]() ,
,
∴DC2=AD·CM=36,
∴DC=6,
∴S矩形ABCD=AD·CD=24.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰△ABC中,AB=AC,BC∥x轴,点A.C在反比例函数y=
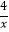 (x>0)的图象上,点B在反比例函数y=
(x>0)的图象上,点B在反比例函数y=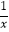 (x>0)的图象上,则△ABC的面积为 .
(x>0)的图象上,则△ABC的面积为 . 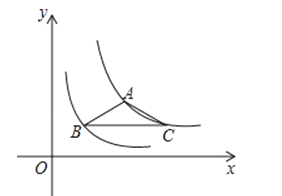
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正比例函数y=
 x与反比例函数y=
x与反比例函数y= (k>0)的图象交于A、B两点,且点A的横坐标为4.
(k>0)的图象交于A、B两点,且点A的横坐标为4.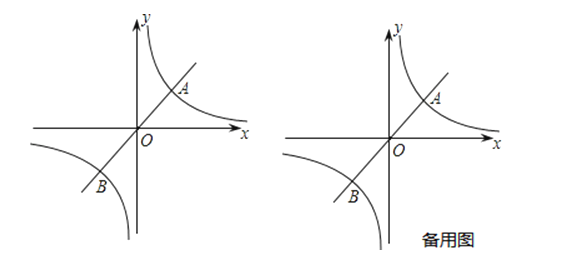
(1)求k的值;
(2)根据图象直接写出正比例函数值小于反比例函数值时x的取值范围;
(3)过原点O的另一条直线l交双曲线y= (k>0)于P、Q两点(P点在第一象限),若由点A、P、B、Q为顶点组成的四边形面积为24,求点P的坐标.
(k>0)于P、Q两点(P点在第一象限),若由点A、P、B、Q为顶点组成的四边形面积为24,求点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】(﹣2)×3的结果( )
A.﹣6
B.6
C.5
D.﹣5 -
科目: 来源: 题型:
查看答案和解析>>【题目】为了加强公民的节水意识,合理利用水资源,某市采用价格调控的手段达到节水的目的,该市自来水收费的收费标准如下表:
收费标准(注:水费按月份结算)
每月用水量
单价(元/立方米)
不超出
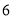 立方米的部分
立方米的部分
超出
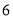 立方米不超出
立方米不超出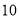 立方米的部分
立方米的部分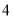
超出
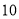 立方米的部分
立方米的部分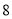
例如:某户居民
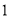 月份用水
月份用水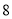 立方米,应收水费为
立方米,应收水费为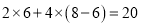 (元).
(元).请根据上表的内容解答下列问题:
(
 )若某户居民
)若某户居民 月份用水
月份用水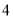 立方米,则应收水费多少元?
立方米,则应收水费多少元?(
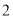 )若某户居民
)若某户居民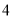 月份用水
月份用水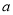 立方米(其中
立方米(其中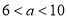 ),请用含
),请用含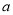 的代数式表示应收水费.
的代数式表示应收水费.(
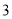 )若某户居民
)若某户居民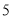 、
、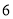 两个月共用水
两个月共用水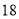 立方米(
立方米(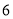 月份用水量超过了
月份用水量超过了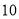 立方米),设
立方米),设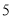 月份用水
月份用水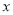 立方米,请用含
立方米,请用含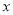 的代数式表示该居民
的代数式表示该居民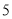 、
、 两个月共交水费多少元.
两个月共交水费多少元. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算(a3b)2÷(ab)2的结果是 ( )
A. a3 B. a4 C. a3b D. a4b
-
科目: 来源: 题型:
查看答案和解析>>【题目】若9x2+mxy+16y2是一个完全平方式,那m的值是( )
A. ±12 B. -12 C. ±24 D. -24
相关试题

