【题目】如图,已知正比例函数y=![]() x与反比例函数y=
x与反比例函数y=![]() (k>0)的图象交于A、B两点,且点A的横坐标为4.
(k>0)的图象交于A、B两点,且点A的横坐标为4.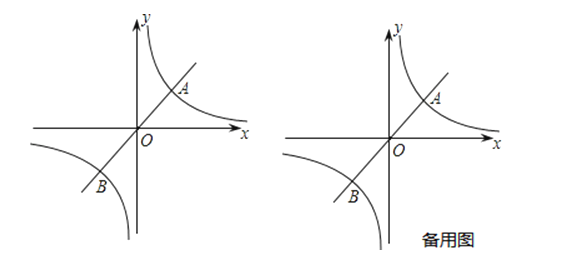
(1)求k的值;
(2)根据图象直接写出正比例函数值小于反比例函数值时x的取值范围;
(3)过原点O的另一条直线l交双曲线y=![]() (k>0)于P、Q两点(P点在第一象限),若由点A、P、B、Q为顶点组成的四边形面积为24,求点P的坐标.
(k>0)于P、Q两点(P点在第一象限),若由点A、P、B、Q为顶点组成的四边形面积为24,求点P的坐标.
参考答案:
【答案】(1)∵点A在正比例函数y=![]() x上,
x上,
∴把x=4代入正比例函数y=![]() x,
x,
解得y=2,∴点A(4,2),
∵点A与B关于原点对称,
∴B点坐标为(﹣4,﹣2),
把点A(4,2)代入反比例函数y=![]() ,得k=8,
,得k=8,
(2)由交点坐标,根据图象直接写出正比例函数值小于反比例函数值时x的取值范围,x<﹣4或0<x<4;
(3)∵反比例函数图象是关于原点O的中心对称图形,
∴OP=OQ,OA=OB,
∴四边形APBQ是平行四边形,
∴S△POA=S平行四边形APBQ×![]() =
=![]() ×24=6,
×24=6,
设点P的横坐标为m(m>0且m≠4),
得P(m,![]() ),
),
过点P、A分别做x轴的垂线,垂足为E、F,
∵点P、A在双曲线上,
∴S△POE=S△AOF=4,
若0<m<4,如图,
∵S△POE+S梯形PEFA=S△POA+S△AOF ,
∴S梯形PEFA=S△POA=6.
∴![]() (2+
(2+![]() )(4﹣m)=6.
)(4﹣m)=6.
∴m1=2,m2=﹣8(舍去),
∴P(2,4);
若m>4,如图,
∵S△AOF+S梯形AFEP=S△AOP+S△POE ,
∴S梯形PEFA=S△POA=6.
∴![]() (2+
(2+![]() )(m﹣4)=6,
)(m﹣4)=6,
解得m1=8,m2=﹣2(舍去),
∴P(8,1).
∴点P的坐标是P(2,4)或P(8,1).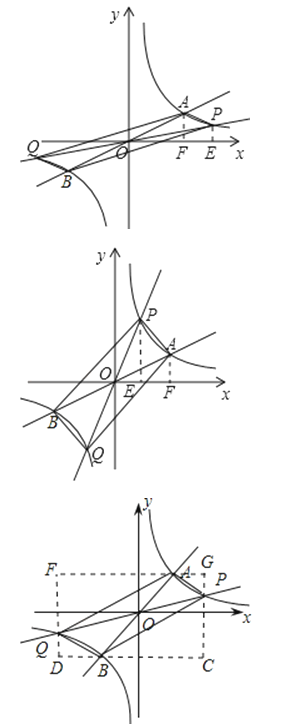
【解析】(1)先将x=4代入正比例函数y=![]() x,可得出y=2,求得点A(4,2),再根据点A与B关于原点对称,得出B点坐标,即可得出k的值;
x,可得出y=2,求得点A(4,2),再根据点A与B关于原点对称,得出B点坐标,即可得出k的值;
(2)正比例函数的值小于反比例函数的值即正比例函数的图象在反比例函数的图象下方,根据图形可知在交点的右边正比例函数的值小于反比例函数的值.
(3)由于双曲线是关于原点的中心对称图形,因此以A、B、P、Q为顶点的四边形应该是平行四边形,那么△POA的面积就应该是四边形面积的四分之一即6.可根据双曲线的解析式设出P点的坐标,然后表示出△POA的面积,由于△POA的面积为6,由此可得出关于P点横坐标的方程,即可求出P点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一个两位数,它的十位数字和个位数字的和为6,则这样的两位数有( )个.
A. 4B. 5C. 6D. 7
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c(a≠0)的开口向上,与x轴交点的横坐标分别为-1、3,则下列说法错误的是( )
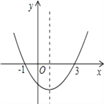
A. 对称轴是直线x=1 B. 方程ax2+bx+c=0的解是x1=-1,x2=3
C. 当x<1,y随x的增大而增大 D. 当-1<x<3时,y<0
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰△ABC中,AB=AC,BC∥x轴,点A.C在反比例函数y=
 (x>0)的图象上,点B在反比例函数y=
(x>0)的图象上,点B在反比例函数y=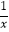 (x>0)的图象上,则△ABC的面积为 .
(x>0)的图象上,则△ABC的面积为 . 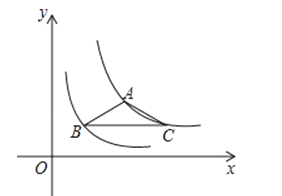
-
科目: 来源: 题型:
查看答案和解析>>【题目】(﹣2)×3的结果( )
A.﹣6
B.6
C.5
D.﹣5 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD为⊙O的内接四边形,且对角线AC为直径,AD=BC,过点D作DG⊥AC,垂足为E,DG分别与AB及CB延长线交于点F、M.
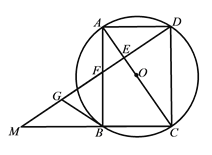
(1)求证:四边形ABCD是矩形;
(2)若点G为MF的中点,求证:BG是⊙O的切线;
(3)若AD=4,CM=9,求四边形ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了加强公民的节水意识,合理利用水资源,某市采用价格调控的手段达到节水的目的,该市自来水收费的收费标准如下表:
收费标准(注:水费按月份结算)
每月用水量
单价(元/立方米)
不超出
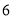 立方米的部分
立方米的部分
超出
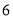 立方米不超出
立方米不超出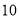 立方米的部分
立方米的部分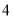
超出
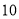 立方米的部分
立方米的部分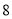
例如:某户居民
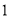 月份用水
月份用水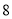 立方米,应收水费为
立方米,应收水费为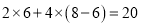 (元).
(元).请根据上表的内容解答下列问题:
(
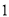 )若某户居民
)若某户居民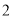 月份用水
月份用水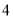 立方米,则应收水费多少元?
立方米,则应收水费多少元?(
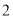 )若某户居民
)若某户居民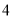 月份用水
月份用水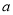 立方米(其中
立方米(其中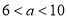 ),请用含
),请用含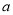 的代数式表示应收水费.
的代数式表示应收水费.(
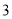 )若某户居民
)若某户居民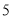 、
、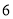 两个月共用水
两个月共用水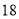 立方米(
立方米(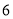 月份用水量超过了
月份用水量超过了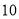 立方米),设
立方米),设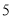 月份用水
月份用水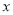 立方米,请用含
立方米,请用含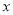 的代数式表示该居民
的代数式表示该居民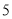 、
、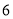 两个月共交水费多少元.
两个月共交水费多少元.
相关试题

