【题目】如图,在Rt△ABC中,AB=AC,D、E是斜边BC上两动点,且∠DAE=45°,将△ABE绕点A逆时针旋转90°后,得到△AFC,连接DF.
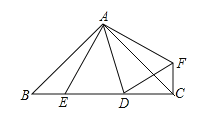
(1)试说明:△AED≌△AFD;
(2)当BE=3,CE=9时,求∠BCF的度数和DE的长;
参考答案:
【答案】(1)见解析;(2)90°,5.
【解析】
(1)根据旋转的性质,可得对应角与对应边相等;根据全等三角形的判定定理即可证明;
(2)设DE=x,则CD=9﹣x.在Rt△DCF中,由DF2=CD2+CF2,CF=BE=3,推出x2=(9﹣x)2+32,解方程即可.
(1)证明:∵将△ABE绕点A逆时针旋转90°后,得到△AFC,
∴△BAE≌△CAF,
∴AE=AF,∠BAE=∠CAF,BE=CF,
∵∠BAC=90°,∠EAD=45°,
∴∠CAD+∠BAE=∠CAD+∠CAF=45°,
∴∠DAE=∠DAF,
∵DA=DA,AE=AF,
∴△AED≌△AFD(SAS);
(2)解:设DE=x,则CD=9﹣x.
∵AB=AC,∠BAC=90°,
∴∠B=∠ACB=45°,
∵∠ABE=∠ACF=45°,
∴∠BCF=90°,
∵△AED≌△AFD,
∴DE=DF=x,
在Rt△DCF中,∵DF2=CD2+CF2,CF=BE=3,
∴x2=(9﹣x)2+32,
∴x=5,
∴DE=5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,
 ,点
,点 ,
, 分别在直线
分别在直线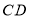 ,
,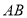 上,
上,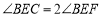 ,过点
,过点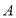 作
作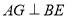 的延长线交于点
的延长线交于点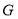 ,交
,交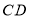 于点
于点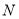 ,
,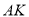 平分
平分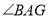 ,交
,交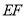 于点
于点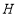 ,交
,交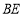 于点
于点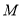 .
.(1)直接写出
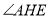 ,
, ,
,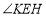 之间的关系:
之间的关系:___________=____________+___________
(2)若
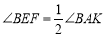 ,求
,求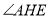 .
.(3)如图2,在(2)的条件下,将
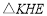 绕着点
绕着点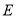 以每秒
以每秒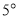 的速度逆时针旋转,旋转时间为
的速度逆时针旋转,旋转时间为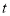 ,当
,当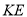 边与射线
边与射线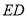 重合时停止,则在旋转过程中,当
重合时停止,则在旋转过程中,当 的其中一边与
的其中一边与 的某一边平行时,直接写出此时
的某一边平行时,直接写出此时 的值.
的值.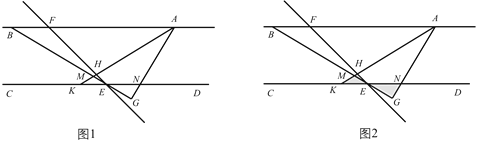
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于二次函数y=x2+mx+1,当0<x≤2时的函数值总是非负数,则实数m的取值范围为( )
A. m≥﹣2 B. ﹣4≤m≤﹣2 C. m≥﹣4 D. m≤﹣4或m≥﹣2
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数
 的部分图象如图,图象过点(﹣1,0),对称轴为直线
的部分图象如图,图象过点(﹣1,0),对称轴为直线 ,下列结论:①
,下列结论:① ;②
;② ;③
;③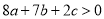 ;④当
;④当 时,
时,  随
随 的增大而增大.其中正确的结论有( )
的增大而增大.其中正确的结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.
(1)求证:△DEF是等腰三角形;
(2)当∠A=50°时,求∠DEF的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(问题情境)
课外兴趣小组活动时,老师提出了如下问题:如图1,△ABC中,若AB=12,AC=8,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长AD到E,使DE=AD,连接BE.请根据小明的方法思考:
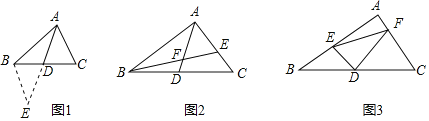
(1)由已知和作图能得到△ADC≌△EDB,依据是 .
A.SSS B.SAS C.AAS D.HL
(2)由“三角形的三边关系”可求得AD的取值范围是 .
解后反思:题目中出现“中点”“中线”等条件,可考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集合到同一个三角形中.
(初步运用)
如图2,AD是△ABC的中线,BE交AC于E,交AD于F,且AE=EF.若EF=3,EC=2,求线段BF的长.
(灵活运用)
如图3,在△ABC中,∠A=90°,D为BC中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF,试猜想线段BE、CF、EF三者之间的等量关系,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,直线l:y=
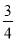 x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=
x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y= x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
x2+bx+c经过点B,与直线l的另一个交点为C(4,n).(1)求n的值和抛物线的解析式;
(2)点D在抛物线上,DE∥y轴交直线l于点E,点F在直线l上,且四边形DFEG为矩形(如图2),设点D的横坐标为t(0<t<4),矩形DFEG的周长为p,求p与t的函数关系式以及p的最大值;
(3)将△AOB绕平面内某点M旋转90°或180°,得到△A1O1B1,点A、O、B的对应点分别是点A1、O1、B1.若△A1O1B1的两个顶点恰好落在抛物线上,那么我们就称这样的点为“落点”,请直接写出“落点”的个数和旋转180°时点A1的横坐标.

相关试题

