【题目】如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.
(1)求证:△DEF是等腰三角形;
(2)当∠A=50°时,求∠DEF的度数.

参考答案:
【答案】(1)证明见解析;(2)65°
【解析】试题分析:⑴由AB=AC,可知∠B=∠ C,根据题意易得△ BDE ≌ △ CEF(SAS),从而得到DE=EF,命题得证.
⑵因为∠ A=50°,所以∠ B=∠ C=65°,由⑴可知,∠BDE=∠CEF,所以∠DEB+∠CEF=
∠DEB+∠ BDE=115°,从而∠ DEF=180°-115°=65°.
试题解析:⑴∵ AB=AC,∴ ∠B=∠ C.
在△ BDE和△ CEF中,
 ,
,
∴ △ BDE ≌ △ CEF(SAS),则DE=EF,故△ DEF是等腰三角形.
⑵在△ABC中,∵∠A=50°,∴∠B=∠C=65°.
∵ △ BDE ≌ △ CEF,∴ ∠BDE=∠CEF,
∴ ∠DEB+∠CEF=∠DEB+∠ BDE=180°-65°=115°,
则 ∠ DEF=180°-(∠DEB+∠CEF)=180°-115°=65°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,点C在线段AB上,AC = 8 cm,CB = 6 cm,点M、N分别是AC、BC的中点.

(1)求线段MN的长.
(2)若C为线段AB上任意一点,满足AC+CB=a(cm),其他条件不变,你能猜想出MN的长度吗?并说明理由.
(3)若C在线段AB的延长线上,且满足AC-CB=b(cm),M、N分别为AC、BC的中点,你能猜想出MN的长度吗?请画出图形,写出你的结论,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠BAC=90°,AD⊥BC,垂足为D.求作∠ABC的平分线,分别交AD,AC于P,Q两点,并证明AP=AQ.(要求:尺规作图,保留作图痕迹,不写作法)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,过边长为3的等边三角形ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,问:若PA=CQ时,连接PQ交AC边于D,求DE的长?

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料,回答提出的问题.
我们知道:一个数
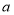 的绝对值可以表示成
的绝对值可以表示成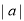 ,它是一个非负数,在数轴上,
,它是一个非负数,在数轴上,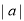 表示
表示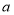 这个数在数轴上所对应的点到原点的距离(距离,当然不可能是负数),这正是绝对值的几何意义,比如说
这个数在数轴上所对应的点到原点的距离(距离,当然不可能是负数),这正是绝对值的几何意义,比如说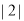 表示2这个数在数轴上所对应的点到原点的距离,它是2,所以说
表示2这个数在数轴上所对应的点到原点的距离,它是2,所以说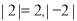 表示
表示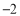 这个数在数轴上所对应的点到原点的距离,它也是2,所以说
这个数在数轴上所对应的点到原点的距离,它也是2,所以说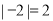 ,严格来说,在数轴上,一个数
,严格来说,在数轴上,一个数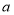 在数轴上所对应的点到原点(原点对应的数为0)的距离应该表示为
在数轴上所对应的点到原点(原点对应的数为0)的距离应该表示为 ,但平时我们都写成
,但平时我们都写成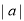 ,原因你明白.
,原因你明白.(1)若给定
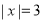 ,要找这样的x,请按照上面材料中的说法,解释它的几何意义并找出对应的
,要找这样的x,请按照上面材料中的说法,解释它的几何意义并找出对应的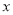 ;
;(2)实际上,对于数轴上任意两个数
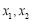 之间的距离我们也可以表示为
之间的距离我们也可以表示为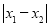 ,反过来,
,反过来,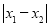 这个绝对值的几何意义就是:数轴上表示
这个绝对值的几何意义就是:数轴上表示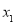 与
与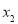 这两个数的点之间的距离,你能结合上面的叙述,解释
这两个数的点之间的距离,你能结合上面的叙述,解释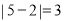 的几何意义吗?请按你的理解说明:
的几何意义吗?请按你的理解说明: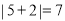 呢,如果能解释这个,你了不起;
呢,如果能解释这个,你了不起;(3)若
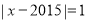 ,请直接写出
,请直接写出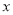 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】从正五边形的五个顶点中,任取四个顶点连成四边形,对于事件M:“这个四边形是等腰梯形” .下列判断正确的是( )
A. 事件M是不可能事件 B. 事件M是必然事件
C. 事件M发生的概率为
 D. 事件M发生的概率为
D. 事件M发生的概率为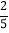
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在4×4的正方形网格中,每个小正方形的顶点称为格点,每个小正方形的边长均为1.在图①,图②中已画出线段AB,在图③中已画出点A.按下列要求画图:
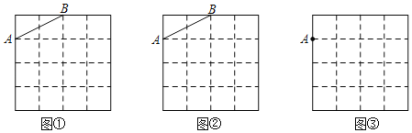
(1)在图①中,以格点为顶点,AB为一边画一个等腰三角形ABC;
(2)在图②中,以格点为顶点,AB为一边画一个正方形;
(3)在图③中,以点A为一个顶点,另外三个顶点也在格点上,画一个面积最大的正方形,这个正方形的面积= .
相关试题

