【题目】如图1,直线l:y=![]() x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=
x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=![]() x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
(1)求n的值和抛物线的解析式;
(2)点D在抛物线上,DE∥y轴交直线l于点E,点F在直线l上,且四边形DFEG为矩形(如图2),设点D的横坐标为t(0<t<4),矩形DFEG的周长为p,求p与t的函数关系式以及p的最大值;
(3)将△AOB绕平面内某点M旋转90°或180°,得到△A1O1B1,点A、O、B的对应点分别是点A1、O1、B1.若△A1O1B1的两个顶点恰好落在抛物线上,那么我们就称这样的点为“落点”,请直接写出“落点”的个数和旋转180°时点A1的横坐标.

参考答案:
【答案】(1)抛物线的解析式为y=![]() x2﹣
x2﹣![]() x﹣1;(2)p=﹣
x﹣1;(2)p=﹣![]() (t﹣2)2+
(t﹣2)2+![]() ,当t=2时,p有最大值
,当t=2时,p有最大值![]() .(3)“落点”的个数有4个,点A1坐标为(
.(3)“落点”的个数有4个,点A1坐标为(![]() ,0)或(
,0)或(![]() ).
).
【解析】
试题分析:(1)把点B的坐标代入直线解析式求出m的值,再把点C的坐标代入直线求解即可得到n的值,然后利用待定系数法求二次函数解析式解答;(2)令y=0求出点A的坐标,从而得到OA、OB的长度,利用勾股定理列式求出AB的长,然后根据两直线平行,内错角相等可得∠ABO=∠DEF,再解直角三角形用DE表示出EF、DF,根据矩形的周长公式表示出p,利用直线和抛物线的解析式表示DE的长,整理即可得到P与t的关系式,再利用二次函数的最值问题解答;(3)根据逆时针旋转角为90°可得A1O1∥y轴时,B1O1∥x轴,旋转角是180°判断出A1O1在x轴上,B1O1∥y轴,根据B1纵坐标为1,求出B1横坐标即可解决问题.
试题解析:(1)∵直线l:y=![]() x+m经过点B(0,﹣1),
x+m经过点B(0,﹣1),
∴m=﹣1,
∴直线l的解析式为y=![]() x﹣1,
x﹣1,
∵直线l:y=![]() x﹣1经过点C(4,n),
x﹣1经过点C(4,n),
∴n=![]() ×4﹣1=2,
×4﹣1=2,
∵抛物线y=![]() x2+bx+c经过点C(4,2)和点B(0,﹣1),
x2+bx+c经过点C(4,2)和点B(0,﹣1),
∴ ,
,
解得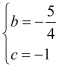 ,
,
∴抛物线的解析式为y=![]() x2﹣
x2﹣![]() x﹣1;
x﹣1;
(2)令y=0,则![]() x﹣1=0,
x﹣1=0,
解得x=![]() ,
,
∴点A的坐标为(![]() ,0),
,0),
∴OA=![]() ,
,
在Rt△OAB中,OB=1,
∴AB=![]() =
=![]() ,
,
∵DE∥y轴,
∴∠ABO=∠DEF,
在矩形DFEG中,EF=DEcos∠DEF=DE![]() =
=![]() DE,
DE,
DF=DEsin∠DEF=DE![]() =
=![]() DE,
DE,
∴p=2(DF+EF)=2(![]() +
+![]() )DE=
)DE=![]() DE,
DE,
∵点D的横坐标为t(0<t<4),
∴D(t,![]() t2﹣
t2﹣![]() t﹣1),E(t,
t﹣1),E(t,![]() t﹣1),
t﹣1),
∴DE=(![]() t﹣1)﹣(
t﹣1)﹣(![]() t2﹣
t2﹣![]() t﹣1)=﹣
t﹣1)=﹣![]() t2+2t,
t2+2t,
∴p=![]() ×(﹣
×(﹣![]() t2+2t)=﹣
t2+2t)=﹣![]() t2+
t2+![]() t,
t,
∵p=﹣![]() (t﹣2)2+
(t﹣2)2+![]() ,且﹣
,且﹣![]() <0,
<0,
∴当t=2时,p有最大值![]() .
.
(3)“落点”的个数有4个,如图1,图2,图3,图4所示.
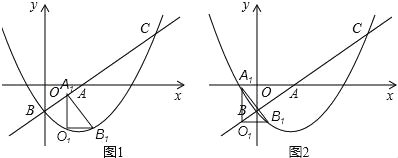
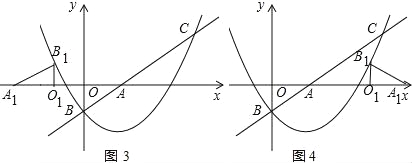
如图3,图4中,B1O1=BO=1,则![]() x2﹣
x2﹣![]() x﹣1=1,解得x=
x﹣1=1,解得x=![]() ,
,
∵A1O1=![]() ,
,
∴图3中,OA1=OO1+A1O1═![]() ,图4中OA1═OO1+O1A1=
,图4中OA1═OO1+O1A1=![]()
∴点A1坐标为(![]() ,0)或(
,0)或(![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】 “囧”(jiong)是近时期网络流行语,像一个人脸郁闷的神情.如图所示,一张边长为20的正方形的纸片,剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案(阴影部分).设剪去的小长方形长和宽分别为x、y,剪去的两个小直角三角形的两直角边长也分别为x、y.
(1)用含有x、y的代数式表示右图中“囧”的面积;
(2)当
 时,求此时“囧”的面积.
时,求此时“囧”的面积.
-
科目: 来源: 题型:
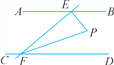
查看答案和解析>>【题目】如图,已知AB∥CD,EF与AB,CD分别相交于点E,F,EP⊥EF,与∠EFD的平分线FP相交于点P,且∠BEP=50°,求∠EPF的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一楼房AB后有一假山,其坡度为i=1:
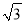 ,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高.(注:坡度i是指坡面的铅直高度与水平宽度的比)
,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高.(注:坡度i是指坡面的铅直高度与水平宽度的比)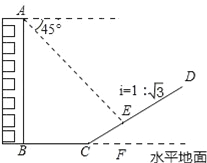
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:有理数m所表示的点到点2距离3个单位,a、b互为相反数,且都不为零,c、d互为倒数.
(1)求m的值;
(2)求代数式:2(a+b)+(
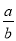 ﹣3cd)﹣m的值.
﹣3cd)﹣m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】若a的相反数是﹣3,b的绝对值是4,且|b|=﹣b,则a﹣b=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程:x2﹣(m﹣3)x﹣m=0.
(1)试判断原方程根的情况;
(2)若抛物线y=x2﹣(m﹣3)x﹣m与x轴交于A(x1,0),B(x2,0)两点,则A,B两点间的距离是否存在最大或最小值?若存在,求出这个值;若不存在,请说明理由.
(友情提示:AB=|x2﹣x1|)
相关试题

