【题目】根据题意解答
(1)已知x= ![]() +1,y=
+1,y= ![]() ﹣1,求下列各式的值. ①x2+2xy+y2
﹣1,求下列各式的值. ①x2+2xy+y2
②x2﹣y2
(2)先化简,再求值: ![]() ÷(
÷( ![]() ﹣a),其中a=
﹣a),其中a= ![]() ﹣2.
﹣2.
参考答案:
【答案】
(1)解:①∵x= ![]() +1,y=
+1,y= ![]() ﹣1,
﹣1,
∴x+y= ![]() ,x﹣y=
,x﹣y= ![]() ,
,
∴ ![]() =12;
=12;
②∵x= ![]() +1,y=
+1,y= ![]() ﹣1,
﹣1,
∴x+y= ![]() ,x﹣y=
,x﹣y= ![]() ,
,
∴x2﹣y2=(x+y)(x﹣y)= ![]()
(2)解: ![]() ÷(
÷( ![]() ﹣a)
﹣a)
= ![]()
= ![]()
= ![]() ,
,
当a= ![]() 时,原式=
时,原式= ![]()
【解析】(1)①根据题目中x、y的值可以求得x+y的值,从而可以解答本题;②根据题目中x、y的值可以求得x+y和x﹣y的值,从而可以解答本题;(2)先化简题目中的式子,再把a的值代入化简后的式子即可解答本题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
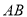 、
、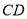 相交于点
相交于点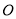 ,
, 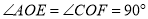 .
.(
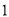 )
) 的余角是__________(填写所有符合要求的角).
的余角是__________(填写所有符合要求的角).(
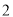 )若
)若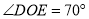 ,求
,求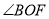 的度数.
的度数.(3)若
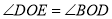 ,求
,求 的度数.
的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知(x﹣y﹣2)2+|x+y+2|=0,则x2﹣y2=__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式:3﹣2(x﹣1)<1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】知识的迁移与应用
问题一:甲、乙两车分别从相距180km的 A、B两地出发,甲车速度为36 km/h,乙车速度为24km/h,两车同时出发,相向而行, 后两车相距120 km?
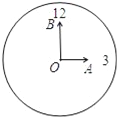
问题二:将线段弯曲后可视作钟表的一部分,如图,在一个圆形时钟的表面上,OA表示时针,OB表示分针(O为两针的旋转中心).下午3点时,OA与OB成直角.
(1)3:40时,时针与分针所成的角度 ;
(2)分针每分钟转过的角度为 ,时针每分钟转过的角度为 ;
(3)在下午3点至4点之间,从下午3点开始,经过多少分钟,时针与分针成60°角?
-
科目: 来源: 题型:
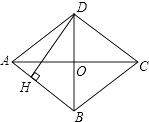
查看答案和解析>>【题目】四边形ABCD是菱形,对角线AC=8cm,BD=6cm,DH⊥AB于H,求DH的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N.
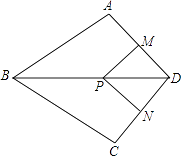
(1)求证:∠ADB=∠CDB;
(2)若∠ADC=90°,求证:四边形MPND是正方形.
相关试题

