【题目】如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N. 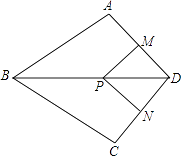
(1)求证:∠ADB=∠CDB;
(2)若∠ADC=90°,求证:四边形MPND是正方形.
参考答案:
【答案】
(1)证明:∵对角线BD平分∠ABC,
∴∠ABD=∠CBD,
在△ABD和△CBD中,
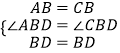 ,
,
∴△ABD≌△CBD(SAS),
∴∠ADB=∠CDB
(2)证明:∵PM⊥AD,PN⊥CD,
∴∠PMD=∠PND=90°,
∵∠ADC=90°,
∴四边形MPND是矩形,
∵∠ADB=∠CDB,
∴∠ADB=45°
∴PM=MD,
∴四边形MPND是正方形.
【解析】(1)根据角平分线的性质和全等三角形的判定方法证明△ABD≌△CBD,由全等三角形的性质即可得到:∠ADB=∠CDB;(2)若∠ADC=90°,由(1)中的条件可得四边形MPND是矩形,再根据两边相等的四边形是正方形即可证明四边形MPND是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据题意解答
(1)已知x=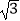 +1,y=
+1,y= 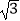 ﹣1,求下列各式的值. ①x2+2xy+y2
﹣1,求下列各式的值. ①x2+2xy+y2
②x2﹣y2
(2)先化简,再求值: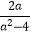 ÷(
÷( 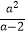 ﹣a),其中a=
﹣a),其中a= 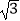 ﹣2.
﹣2. -
科目: 来源: 题型:
查看答案和解析>>【题目】知识的迁移与应用
问题一:甲、乙两车分别从相距180km的 A、B两地出发,甲车速度为36 km/h,乙车速度为24km/h,两车同时出发,相向而行, 后两车相距120 km?
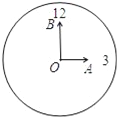
问题二:将线段弯曲后可视作钟表的一部分,如图,在一个圆形时钟的表面上,OA表示时针,OB表示分针(O为两针的旋转中心).下午3点时,OA与OB成直角.
(1)3:40时,时针与分针所成的角度 ;
(2)分针每分钟转过的角度为 ,时针每分钟转过的角度为 ;
(3)在下午3点至4点之间,从下午3点开始,经过多少分钟,时针与分针成60°角?
-
科目: 来源: 题型:
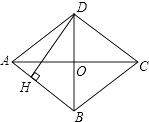
查看答案和解析>>【题目】四边形ABCD是菱形,对角线AC=8cm,BD=6cm,DH⊥AB于H,求DH的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“4000辆自行车、187个服务网点”,台州市区现已实现公共自行车服务全覆盖,为人们的生活带来了方便.图①是公共自行车的实物图,图②是公共自行车的车架示意图,点A、D、C、E在同一条直线上,CD=30cm,DF=20cm,AF=25cm,FD⊥AE于点D,座杆CE=15cm,且∠EAB=75°.
(1)求AD的长;
(2)求点E到AB的距离.(参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,Rt△ABC中,∠ACB=Rt∠,AC=8,BC=6,点D为AB的中点,动点P从点A出发,沿AC方向以每秒1个单位的速度向终点C运动,同时动点Q从点C出发,以每秒2个单位的速度先沿CB方向运动到点B,再沿BA方向向终点A运动,以DP,DQ为邻边构造PEQD,设点P运动的时间为t秒.
(1)当t=2时,求PD的长;
(2)如图2,当点Q运动至点B时,连结DE,求证:DE∥AP.
(3)如图3,连结CD.
①当点E恰好落在△ACD的边上时,求所有满足要求的t值;
②记运动过程中PEQD的面积为S,PEQD与△ACD的重叠部分面积为S1,当
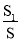 <
<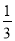 时,请直接写出t的取值范围是 ______ .
时,请直接写出t的取值范围是 ______ .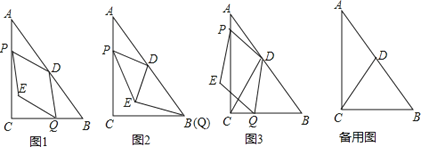
-
科目: 来源: 题型:
查看答案和解析>>【题目】证明一个四边形是正方形,使用次数最少的方法对折,则应该对折( )
A.1次B.2次C.3次D.4次
相关试题

