【题目】如图,在平面直角坐标系中,一动点从原点O出发,按向上,向右,向下,向右的方向不断地移动,每移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),那么A2020坐标为( )

A.(2020,1)B.(2020,0)C.(1010,1)D.(1010,0)
参考答案:
【答案】D
【解析】
结合图象可知:纵坐标每四个点循环一次;由A4(2,0),A8(4,0),A12(6,0)…可得到以下规律,A4n(2n,1)( n为不为0的自然数),从而求解.
由图象可知:纵坐标每四个点循环一次,而2020=505×4,
故A2020的纵坐标与A4的纵坐标相同,都等于0;
由A4(2,0),A8(4,0),A12(6,0)…,
可得到规律A4n(2n,1)( n为不为0的自然数),
当n=505时,A2020(1010,0).
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:A(0,1),B(2,0),C(4,3)
(1)在直角坐标系中描出各点,画出△ABC.
(2)求△ABC的面积;
(3)设点P在坐标轴上,且△ABP与△ABC的面积相等,求点P的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道,在数轴上,|a|表示数a到原点的距离,这是绝对值的几 何意义,进一步地,数轴上两个点A、B,分别用a 和b 表示,那么A、B两点之间的距离为AB=|a﹣b|利用此结论,回答以下问题:
(1)数轴上表示3 和7 的两点之间的距离是 ,数轴上表示﹣3 和﹣7 的两 点之间的距离是 ,数轴上表示2 和﹣3 的两点之间的距离是 ;
(2)数轴上表示x和﹣5 的两点A、B之间的距离是 ,如果|AB|=3,那 么x的值为 ;
(3)当代数式|x﹣1|+|x﹣3|取最小值时,相应的x的取值范围是多少?最小值是多少?
(4)已知点A在数轴上对应的数是a,点B在数轴上对应的数是b,且|a+4|+(b﹣1)2=0,设点P在数轴上对应的数是x,当|PA|﹣|PB|=2时,求x的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,∠BOC=60°,顶点C的坐标为(m,3
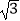 ),反比例函数y=
),反比例函数y= 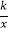 的图象与菱形对角线AO交D点,连接BD,当DB⊥x轴时,k的值是( )
的图象与菱形对角线AO交D点,连接BD,当DB⊥x轴时,k的值是( )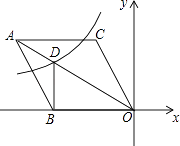
A.6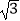
B.﹣6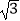
C.12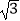
D.﹣12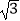
-
科目: 来源: 题型:
查看答案和解析>>【题目】为弘扬中华传统文化,某校组织八年级1000名学生参加汉字听写大赛.为了解学生整体听写能力,从中抽取部分学生的成绩(得分取正整数,满分为100分)进行统计分析,请根据尚未完成的下列图表,解答下列问题:
组别
分数段
频数
频率
一
50.5~60.5
16
0.08
二
60.5~70.5
30
0.15
三
70.5~80.5
m
0.25
四
80.5~90.5
80
n
五
90.5~100.5
24
0.12
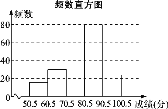
(1)写出表中:m,n,此样本中成绩的中位数落在第几组内;
(2)补全频数直方图;
(3)若成绩超过80分为优秀,该校八年级学生中汉字听写能力优秀的约有多少人?
-
科目: 来源: 题型:
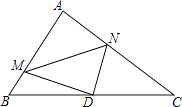
查看答案和解析>>【题目】如图,在Rt△ABC中,∠A=90°,AB=6,AC=8,点D为边BC的中点,点M为边AB上的一动点,点N为边AC上的一动点,且∠MDN=90°,则cos∠DMN为( )
A.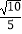
B.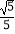
C.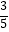
D.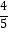
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c的部分图象如图所示,则关于x的方程ax2+bx+c=0的两个根的和为 .
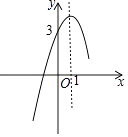
相关试题

