【题目】如图,在平面坐标系中,点![]() 、点
、点![]() 分别在
分别在![]() 轴、
轴、![]() 轴的正半轴上,且
轴的正半轴上,且![]() ,另有两点
,另有两点![]() 和
和![]() ,
,![]() 、
、![]() 均大于
均大于![]() ;
;
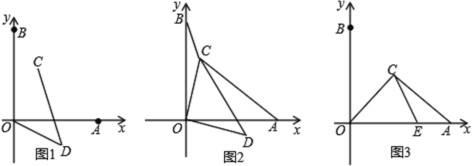
(1)连接![]() 、
、![]() ,求证:
,求证:![]() ;
;
(2)连接![]() 、
、![]() 、
、![]() ,若
,若![]() ,
,![]() ,
,![]() ,求
,求![]() 的度数;
的度数;
(3)若![]() ,在线段
,在线段![]() 上有一点
上有一点![]() ,且
,且![]() ,
,![]() ,
,![]() ,求
,求![]() 的面积.
的面积.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 的面积
的面积![]() .
.
【解析】
(1)过C点、D点向x轴、y轴作垂线,运用勾股定理计算,结合全等可证;
(2)连接DA,证△OCB≌△ODA(SAS),可得AD=CB=1,而OC=OD=2,故CD=2![]() ,根据勾股定理逆定理可证∠ADC=90°,易得∠OCB=∠ODA=135°;
,根据勾股定理逆定理可证∠ADC=90°,易得∠OCB=∠ODA=135°;
(3)作CF⊥OA,F为垂足,有CF2=CE2-EF2,CF2=CA2-AF2=CA2-(AE+EF)2,设EF=x,列出关于x的方程,求得x=![]() ,再在Rt△CEF中,根据勾股定理求得CF=
,再在Rt△CEF中,根据勾股定理求得CF=![]()
![]() ,然后由三角形的面积公式即可求解.
,然后由三角形的面积公式即可求解.
(1)证明:过![]() 点、
点、![]() 点向
点向![]() 轴、
轴、![]() 轴作垂线,垂足分别为
轴作垂线,垂足分别为![]() 、
、![]() .
.
![]() ,
,![]() ,
,![]() 、
、![]() 均大于
均大于![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() 是等腰直角三角形,
是等腰直角三角形,
![]() ;
;
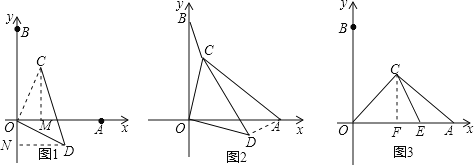
(2)解:连接![]() .
.
在![]() 与
与![]() 中,
中,
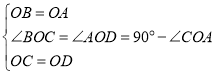 ,
,
![]() ,
,
![]() ,
,![]() .
.
![]() ,
,
![]() .
.
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
(3)解:作![]() ,
,![]() 为垂足,由勾股定理得
为垂足,由勾股定理得
![]() ,
,![]() ,
,
设![]() ,可得
,可得![]() ,
,
解得![]() .
.
在![]() 中,得
中,得![]() ,
,
![]() ,
,
![]() 的面积
的面积![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一圆桌周围有5个箱子 ,依顺时针方向编号1 ~5 ,小明从1号箱子 沿着圆桌依顺时针方向前进,每经过-个箱子就丢入-颗球,所有小球共有红、黄、绿3种颜色, 1号箱子红色, 2号箱子黄色, 3号箱子绿色, 4号红色, 5号黄色, 1号绿色..... ,颜色依次循环,当他围绕圆桌刚好丢完2020圈时,则第5号箱子有( ) 个红球.
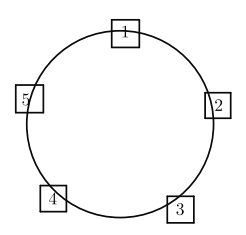
A.672B.673C.674D.675
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,D为⊙O上一点,点C在直径BA的延长线上,∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,若BC=9,tan∠CDA=
 ,求BE的长.
,求BE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】[阅读]
在平面直角坐标系中,以任意两点P( x1,y1)、Q(x2,y2)为端点的线段中点坐标为(
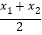 ,
,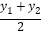 ).
).[运用]
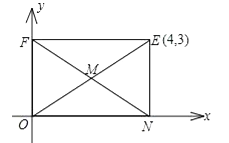
(1)如图,矩形ONEF的对角线相交于点M,ON、OF分别在x轴和y轴上,O为坐标原点,点E的坐标为(4,3),则点M的坐标为 .
(2)在直角坐标系中,有A(﹣1,2),B(3,1),C(1,4)三点,另有一点D与点A、B、C构成平行四边形的顶点,求点D的坐标.
-
科目: 来源: 题型:
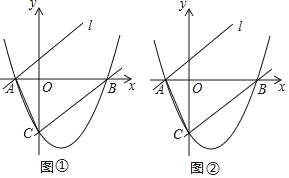
查看答案和解析>>【题目】如图所示,抛物线y=
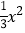 ﹣
﹣ x﹣4与x轴交于点A、B,与y 轴相交于点C.
x﹣4与x轴交于点A、B,与y 轴相交于点C.(1)求直线BC的解析式;
(2)将直线BC向上平移后经过点A得到直线l:y=mx+n,点D在直线l上,若以A、B、C、D为顶点的四边形是平行四边形,求出点D的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)
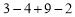 .
.(2)
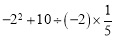 .
.(3)
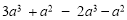 .
.(4)
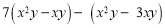 .
.(5)解方程
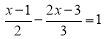
(6)解方程组
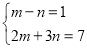
-
科目: 来源: 题型:
查看答案和解析>>【题目】矩形OABC在平面直角坐标系中的位置如图所示,点B的坐标为(3,4),点D的坐标为(2,0),E为AB上的点,当△CDE的周长最小时,点E的坐标为( )
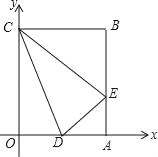
A. (1,3) B. (3,1) C. (4,1) D. (3,2)
相关试题

