【题目】扑克牌游戏:小明背对小亮,让小亮按下列四个步骤操作:
第一步,分发左、中、右三堆牌,每堆牌不少于两张,且各堆牌的张数相同;
第二步,从左边一堆拿出两张,放入中间一堆;
第三步,从右边一堆拿出一张,放入中间一堆;
第四步,左边一堆有几张牌,就从中间一堆拿出几张牌放入左边一堆.
这时,小明准确地说出了中间一堆牌现有的张数,聪明的你,你认为中间一堆牌的张数是多少?
【答案】5
【解析】
此题看似复杂,其实只是考查了整式的基本运算.把每堆牌的数量用相应的字母表示出来,列式表示变化情况即可找出最后答案.
解答:解:设第一步时候,每堆牌的数量都是x(x≥2);
第二步时候:左边x-2,中间x+2,右边x;
第三步时候:左边x-2,中级x+3,右边x-1;
第四步开始时候,左边有(x-2)张牌,则从中间拿走(x-2)张,则中间所剩牌数为(x+3)-(x-2)=x+3-x+2=5.
所以中间一堆牌此时有5张牌.
【题型】填空题
【结束】
44
【题目】为什么总是1 089?
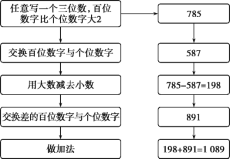
用不同的三位数再试几次,结果都是1 089吗?你能发现其中的原因吗?
参考答案:
【答案】结果都是1089,理由见解析
【解析】
设一个三位数为100a+10b+c,且a=c+2,可得原数为101c+10b+200,
交换百位数字与个位数字后的三位数为100c+10b+a,即为100c+10b+c+2=101c+10b+2,
所以大数减小数为198,可得交换前后的两个三位数,可得答案.
结果都是1 089.
原因:设一个三位数为100a+10b+c,且a=c+2,
所以100a+10b+c=100(c+2)+10b+c=101c+10b+200;
交换百位数字与个位数字后的三位数为100c+10b+a,即为100c+10b+c+2=101c+10b+2.
所以大数减小数为101c+10b+200-(101c+10b+2)=198.
所以将差的百位数字与个位数字交换后的三位数为891,198+891=1089.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在锐角△ABC中,D,E分别为AB,BC中点,F为AC上一点,且∠AFE=∠A,DM∥EF交AC于点M.

(1)求证:DM=DA;
(2)点G在BE上,且∠BDG=∠C,如图②,求证:△DEG∽△ECF;
(3)在图②中,取CE上一点H,使∠CFH=∠B,若BG=1,求EH的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
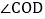 在
在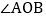 的内部,OM平分
的内部,OM平分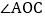 ,ON平分
,ON平分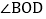
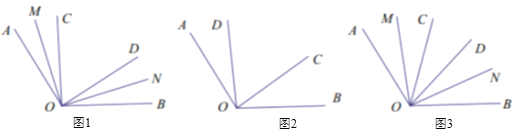
(1)如图1,
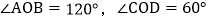 时,当OC在OD的左侧,求
时,当OC在OD的左侧,求 的度数.
的度数.(2)如图2,
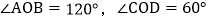 时,当OC在OD的右侧 ,请补全图形,并求
时,当OC在OD的右侧 ,请补全图形,并求 的度数.
的度数.(3)如图3,当
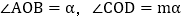 ,且OC在OD左侧时,试用
,且OC在OD左侧时,试用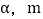 的代数式表示
的代数式表示 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,O为原点,直线y=﹣2x﹣1与y轴交于点A,与直线y=﹣x交于点B,点B关于原点的对称点为点C.
(Ⅰ)求过B,C两点的抛物线y=ax2+bx﹣1解析式;
(Ⅱ)P为抛物线上一点,它关于原点的对称点为Q.
①当四边形PBQC为菱形时,求点P的坐标;
②若点P的横坐标为t(﹣1<t<1),当t为何值时,四边形PBQC面积最大?最大值是多少?并说明理由.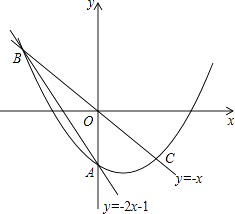
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a<b,则下列各式中,错误的是( )
A.a﹣3<b﹣3
B.﹣a<﹣b
C.﹣2a>﹣2b
D. a<
a<  b
b -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=x2﹣4x与x轴交于O,A两点,P为抛物线上一点,过点P的直线y=x+m与对称轴交于点Q
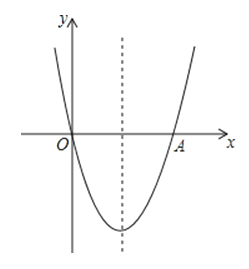
(1)这条抛物线的对称轴是 ,直线PQ与x轴所夹锐角的度数是 .
(2)若两个三角形面积满足S△POQ= S△PAQ , 求m的值
S△PAQ , 求m的值
(3)当点P在x轴下方的抛物线上时,过点C(2,2)的直线AC与直线PQ交于点D,求:①PD+DQ的最大值;②PDDQ的最大值. -
科目: 来源: 题型:
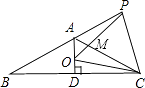
查看答案和解析>>【题目】如图,已知等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下面的结论:①∠APO+∠DCO=30°;②△OPC是等边三角形;③AC=AO+AP;④S△ABC=S四边形AOCP , 其中正确的个数是( )
A.1
B.2
C.3
D.4
相关试题

