【题目】如图,抛物线y=x2﹣4x与x轴交于O,A两点,P为抛物线上一点,过点P的直线y=x+m与对称轴交于点Q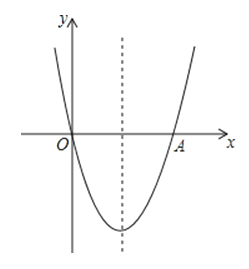
(1)这条抛物线的对称轴是 ,直线PQ与x轴所夹锐角的度数是 .
(2)若两个三角形面积满足S△POQ=![]() S△PAQ , 求m的值
S△PAQ , 求m的值
(3)当点P在x轴下方的抛物线上时,过点C(2,2)的直线AC与直线PQ交于点D,求:①PD+DQ的最大值;②PDDQ的最大值.
参考答案:
【答案】
(1)2;![]()
(2)
设直线PQ交x轴于点B,分别过O点,A点作PQ的垂线,垂足分别是E、F,显然当点B在OA的延长线时,S△POQ=![]() S△PAQ不成立;
S△PAQ不成立;
①当点B落在线段OA上时,如图①,

![]() =
=![]() =
=![]() ,
,
由△OBE∽△ABF得,![]() =
=![]() =
=![]() ,
,
∴AB=3OB,
∴OB=![]() OA,
OA,
由y=x2﹣4x得点A(4,0),
∴OB=1,
∴B(1,0),
∴1+m=0,
∴m=﹣1;
②当点B落在线段AO的延长线上时,如图②,
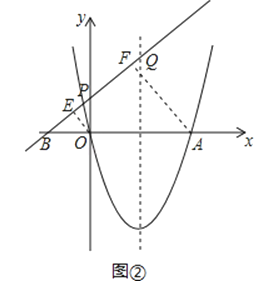
同理可得OB=![]() OA=2,
OA=2,
∴B(﹣2,0),
∴﹣2+m=0,
∴m=2,
综上,当m=﹣1或2时,S△POQ=![]() S△PAQ;
S△PAQ;
(3)
①过点C作CH∥x轴交直线PQ于点H,如图③,
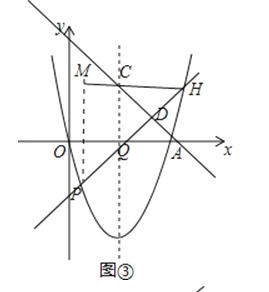
可得△CHQ是等腰三角形,
∵∠CDQ=45°+45°=90°,
∴AD⊥PH,
∴DQ=DH,
∴PD+DQ=PH,
过P点作PM⊥CH于点M,则△PMH是等腰直角三角形,
∴PH=![]() PM,
PM,
∴当PM最大时,PH最大,
∴当点P在抛物线顶点出时,PM最大,此时PM=6,
∴PH的最大值为![]() ,
,
即PD+DQ的最大值为![]() .
.
②由①可知:PD+DQ≤![]() ,
,
设PD=a,则DQ![]() ﹣a,
﹣a,
∴PDDQ≤a(![]() ﹣a)=﹣a2+
﹣a)=﹣a2+![]() a=﹣(a﹣
a=﹣(a﹣![]() )2+18,
)2+18,
∵当点P在抛物线的顶点时,a=![]() ,
,
∴PDDQ≤18.
∴PDDQ的最大值为18.
【解析】解:(1)∵y=x2﹣4x=(x﹣2)2﹣4,
∴抛物线的对称轴是x=2,
∵直线y=x+m,
∴直线与坐标轴的交点坐标为(﹣m,0),(0,m),
∴交点到原点的距离相等,
∴直线与坐标轴围成的三角形是等腰直角三角形,
∴直线PQ与x轴所夹锐角的度数是45°,
故答案为x=2、45°.
(1)把抛物线的解析式化成顶点式即可求得对称轴;求得直线与坐标轴的交点坐标,即可证得直线和坐标轴围成的图形是等腰直角三角形,从而求得直线PQ与x轴所夹锐角的度数;
(2)分三种情况分别讨论根据已知条件,通过△OBE∽△ABF对应边成比例即可求得;
(3)①过点C作CH∥x轴交直线PQ于点H,可得△CHQ是等腰三角形,进而得出AD⊥PH,得出DQ=DH,从而得出PD+DQ=PH,过P点作PM⊥CH于点M,则△PMH是等腰直角三角形,得出PH=![]() PM,因为当PM最大时,PH最大,通过求得PM的最大值,从而求得PH的最大值;由①可知:PD+PH≤6
PM,因为当PM最大时,PH最大,通过求得PM的最大值,从而求得PH的最大值;由①可知:PD+PH≤6![]() ,设PD=a,则DQ
,设PD=a,则DQ![]() ﹣a,得出PDDQ≤a(6
﹣a,得出PDDQ≤a(6![]() ﹣a)=﹣a2+6
﹣a)=﹣a2+6![]() a=﹣(a﹣3
a=﹣(a﹣3![]() )2+18,当点P在抛物线的顶点时,a=3
)2+18,当点P在抛物线的顶点时,a=3![]() ,得出PDDQ≤18.
,得出PDDQ≤18.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,O为原点,直线y=﹣2x﹣1与y轴交于点A,与直线y=﹣x交于点B,点B关于原点的对称点为点C.
(Ⅰ)求过B,C两点的抛物线y=ax2+bx﹣1解析式;
(Ⅱ)P为抛物线上一点,它关于原点的对称点为Q.
①当四边形PBQC为菱形时,求点P的坐标;
②若点P的横坐标为t(﹣1<t<1),当t为何值时,四边形PBQC面积最大?最大值是多少?并说明理由.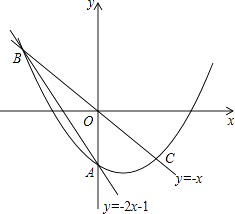
-
科目: 来源: 题型:
查看答案和解析>>【题目】扑克牌游戏:小明背对小亮,让小亮按下列四个步骤操作:
第一步,分发左、中、右三堆牌,每堆牌不少于两张,且各堆牌的张数相同;
第二步,从左边一堆拿出两张,放入中间一堆;
第三步,从右边一堆拿出一张,放入中间一堆;
第四步,左边一堆有几张牌,就从中间一堆拿出几张牌放入左边一堆.
这时,小明准确地说出了中间一堆牌现有的张数,聪明的你,你认为中间一堆牌的张数是多少?
【答案】5
【解析】
此题看似复杂,其实只是考查了整式的基本运算.把每堆牌的数量用相应的字母表示出来,列式表示变化情况即可找出最后答案.
解答:解:设第一步时候,每堆牌的数量都是x(x≥2);
第二步时候:左边x-2,中间x+2,右边x;
第三步时候:左边x-2,中级x+3,右边x-1;
第四步开始时候,左边有(x-2)张牌,则从中间拿走(x-2)张,则中间所剩牌数为(x+3)-(x-2)=x+3-x+2=5.
所以中间一堆牌此时有5张牌.
【题型】填空题
【结束】
44【题目】为什么总是1 089?
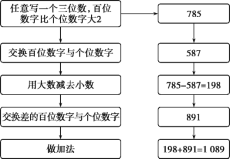
用不同的三位数再试几次,结果都是1 089吗?你能发现其中的原因吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a<b,则下列各式中,错误的是( )
A.a﹣3<b﹣3
B.﹣a<﹣b
C.﹣2a>﹣2b
D. a<
a<  b
b -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下面的结论:①∠APO+∠DCO=30°;②△OPC是等边三角形;③AC=AO+AP;④S△ABC=S四边形AOCP , 其中正确的个数是( )
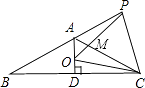
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E,H,G,N在同一直线上,△EFG≌△NMH,∠F和∠M是对应角.在△EFG中,FG是最长边.在△NMH中,MH是最长边.已知EF=2.1 cm,EH=1.1 cm,HN=3.3 cm.
(1)写出其他对应边及对应角;
(2)求线段MN及线段HG的长度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中有一正方形AOBC,反比例函数y=
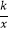 经过正方形AOBC对角线的交点,半径为(6﹣3
经过正方形AOBC对角线的交点,半径为(6﹣3 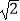 )的圆内切于△ABC,则k的值为 .
)的圆内切于△ABC,则k的值为 . 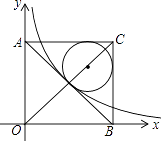
相关试题

