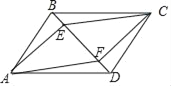
【题目】如图,在ABCD中,经过A,C两点分别作AE⊥BD,CF⊥BD,E,F为垂足.
(1)求证:△AED≌△CFB;
(2)求证:四边形AFCE是平行四边形
参考答案:
【答案】(1)见解析;(2)见解析.
【解析】
(1)根据平行四边形的性质可得AD=BC,∠CBF=∠ADE,再根据垂线的性质可得∠CFB=∠AED=90°,再根据全等三角形的判定(角角边)来证明即可;
(2)根据全等三角形的性质可得AE=CF,再由AE⊥BD,CF⊥BD可得AE∥CF,根据一组对边平行且相等的四边形为平行四边形即可证明.
(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠CBF=∠ADE,
∵AE⊥BD,CF⊥BD,
∴∠CFB=∠AED=90°,
∴△AED≌△CFB(AAS).
(2)证明:∵△AED≌△CFB,
∴AE=CF,
∵AE⊥BD,CF⊥BD,
∴AE∥CF,
∴四边形AFCE是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知正方形ABCO,A(0,3),点D为x轴上一动点,以AD为边在AD的右侧作等腰Rt△ADE,∠ADE=90°,连接OE,则OE的最小值为( )
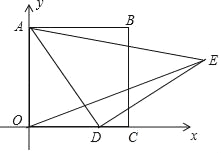
A.
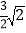 B.
B. 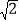 C. 2
C. 2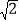 D. 3
D. 3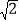
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,购买“黄金1号”王米种子,所付款金额y元与购买量x(千克)之间的函数图象由线段OA和射线AB组成,则购买1千克“黄金1号”玉米种子需付款___元,购买4千克“黄金1号”玉米种子需___元.
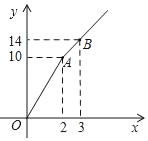
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ABC=90°,∠ACB=30°,AB=2cm,E、F分别是AB、AC的中点,动点P从点E出发,沿EF方向匀速运动,速度为1cm/s,同时动点Q从点B出发,沿BF方向匀速运动,速度为2cm/s,连接PQ,设运动时间为ts(0<t<1),则当t=___时,△PQF为等腰三角形.
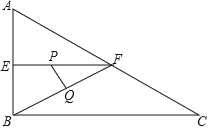
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了绿化环境,某中学八年级(3班)同学都积极参加了植树活动,下面是今年3月份该班同学植树情况的扇形统计图和不完整的条形统计图:
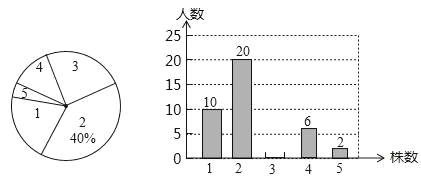
请根据以上统计图中的信息解答下列问题.
(1)植树3株的人数为 ;
(2)扇形统计图中植树为1株的扇形圆心角的度数为 ;
(3)该班同学植树株数的中位数是
(4)小明以下方法计算出该班同学平均植树的株数是:(1+2+3+4+5)÷5=3(株),根据你所学的统计知识
判断小明的计算是否正确,若不正确,请写出正确的算式,并计算出结果
-
科目: 来源: 题型:
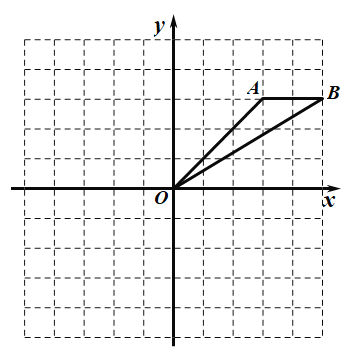
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点A(3,3),B(5,3).
(1)已知点C(2,-4),求四边形AOCB的面积;
(2)将线段OB先向上平移2个单位长度,再向左平移4个单位长度,得到线段O2B2,画出两次平移后的图形,并求线段OB在两次平移过程中扫过的总面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,直线y=kx﹣2k(k<0),与y轴交于点A,与x轴交于点B,AB=2
 .
.
(1)直接写出点A,点B的坐标;
(2)如图2,以AB为边,在第一象限内画出正方形ABCD,求直线DC的解析式;
(3)如图3,(2)中正方形ABCD的对角线AC、BD即交于点G,函数y=mx和y=
 (x≠0)的图象均经过点G,请利用这两个函数的图象,当mx>
(x≠0)的图象均经过点G,请利用这两个函数的图象,当mx> 时,直接写出x的取值范围.
时,直接写出x的取值范围.
相关试题

