【题目】如图,AB是⊙O的直径,点C在⊙O上,∠CAB的平分线交⊙O于点D,过点D作AC的垂线交AC的延长线于点E,连接BC交AD于点F. 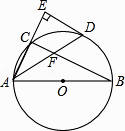
(1)猜想ED与⊙O的位置关系,并证明你的猜想;
(2)若AB=6,AD=5,求AF的长.
参考答案:
【答案】
(1)解:ED与⊙O的位置关系是相切.理由如下:
连接OD,
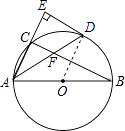
∵∠CAB的平分线交⊙O于点D,
∴ ![]() =
= ![]() ,
,
∴OD⊥BC,
∵AB是⊙O的直径,
∴∠ACB=90°,
即BC⊥AC,
∵DE⊥AC,
∴DE//BC,
∴OD⊥DE,
∴ED与⊙O的位置关系是相切
(2)解:连接BD.
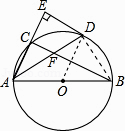
∵AB是直径,
∴∠ADB=90°,
在直角△ABD中,BD= ![]() =
= ![]() =
= ![]() ,
,
∵AB为直径,
∴∠ACB=∠ADB=90°,
又∵∠AFC=∠BFD,
∴∠FBD=∠CAD=∠BAD
∴△FBD∽△BAD,
∴ ![]() =
= ![]()
∴FD= ![]()
∴AF=AD﹣FD=5﹣ ![]() =
= ![]() .
.
【解析】(1)连接OD,根据∠CAB的平分线交⊙O于点D,则 ![]() =
= ![]() ,依据垂径定理可以得到:OD⊥BC,然后根据直径的定义,可以得到OD//AE,从而证得:DE⊥OD,则DE是圆的切线;(2)首先证明△FBD∽△BAD,依据相似三角形的对应边的比相等,即可求DF的长,继而求得答案.
,依据垂径定理可以得到:OD⊥BC,然后根据直径的定义,可以得到OD//AE,从而证得:DE⊥OD,则DE是圆的切线;(2)首先证明△FBD∽△BAD,依据相似三角形的对应边的比相等,即可求DF的长,继而求得答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、B表示的数分别是a、b,点A在0和1对应的两点(不包括这两点)之间移动,点B在﹣3,﹣2对应的两点之间移动,下列四个代数式的值可能比2018大的是( )

A.
 B. b﹣a C. (a﹣b)2 D.
B. b﹣a C. (a﹣b)2 D. 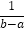
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图, 已知点A、点B是直线上的两点,AB =12厘米,点C在线段AB上,且AC=8厘米.点P、点Q是直线上的两个动点,点P的速度为1厘米/秒,点Q的速度为2厘米/秒.点P、Q分别从点C、点B同时出发,在直线上运动,则经过 秒时线段PQ的长为5厘米.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程2(x+1)﹣m=﹣
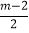 的解比方程5(x﹣1)﹣1=4(x﹣1)+1的解大2.
的解比方程5(x﹣1)﹣1=4(x﹣1)+1的解大2.(1)求第二个方程的解;
(2)求m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某车间有技术工人85人,平均每天每人可加工甲种部件16个或乙种部件10个,2个甲种部件和3个乙种部件配成一套,问加工甲、乙两种部件各安排多少人才能使每天加工的两种部件刚好配套?并求出加工了多少套?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某次学生夏令营活动,有小学生、初中生、高中生和大学生参加,共200人,各类学生人数比例见扇形统计图.
(1)参加这次夏令营活动的初中生共有多少人?
(2)活动组织者号召参加这次夏令营活动的所有学生为贫困学生捐款结果小学生每人捐款5元,初中生每人捐款10元,高中生每人捐款15元,大学生每人捐款20元问平均每人捐款是多少元?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=﹣
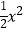 +bx+c图象经过A(﹣1,0),B(4,0)两点.
+bx+c图象经过A(﹣1,0),B(4,0)两点.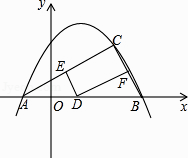
(1)求抛物线的解析式;
(2)若C(m,m﹣1)是抛物线上位于第一象限内的点,D是线段AB上的一个动点(不与A、B重合),过点D分别作DE//BC交AC于E,DF//AC交BC于F.
①求证:四边形DECF是矩形;
②试探究:在点D运动过程中,DE、DF、CF的长度之和是否发生变化?若不变,求出它的值,若变化,试说明变化情况.
相关试题

