【题目】如图,已知抛物线y=﹣ ![]() +bx+c图象经过A(﹣1,0),B(4,0)两点.
+bx+c图象经过A(﹣1,0),B(4,0)两点.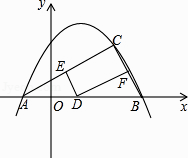
(1)求抛物线的解析式;
(2)若C(m,m﹣1)是抛物线上位于第一象限内的点,D是线段AB上的一个动点(不与A、B重合),过点D分别作DE//BC交AC于E,DF//AC交BC于F.
①求证:四边形DECF是矩形;
②试探究:在点D运动过程中,DE、DF、CF的长度之和是否发生变化?若不变,求出它的值,若变化,试说明变化情况.
参考答案:
【答案】
(1)
解:因为抛物线与x轴交于(﹣1,0)(4,0),可以假设y=a(x+1)(x﹣4)
∵a=﹣ ![]() ,
,
∴y=﹣ ![]() (x+1)(x﹣4)
(x+1)(x﹣4)
即y=﹣ ![]() x2+
x2+ ![]() x+2
x+2
(2)
①证明:把C(m,m﹣1)代入y=﹣ ![]() x2+
x2+ ![]() x+2得
x+2得
m﹣1=﹣ ![]() m2+
m2+ ![]() m+2,
m+2,
∴m1=﹣2,m2=3,
∵C在第一象限,
∴ ![]() ,∴m>1,
,∴m>1,
∴m=﹣2(不符合题意,舍),m=3,
∴C的坐标是(3,2),
∵BC//DE DF//AC,
∴四边形DECF是平行四边形,
∵AB2=25 AC2=20 BC2=5
∴AB2=AC2+BC2,
∴∠ACB=90°,
∴四边形BECF是矩形.
②∵DE//BC,
∴△AED∽△ACB,
∴ ![]() =
= ![]() ①.
①.
同理,得
![]() =
= ![]() ②,
②,
①+②得
![]() +
+ ![]() =
= ![]() =1,
=1,
∵AC=2 ![]() ,BC=
,BC= ![]() ,CF=ED,
,CF=ED,
∴ ![]() +
+ ![]() =1,
=1,
即2ED+DF=2 ![]() ,
,
∴ED+DF+FC=2 ![]() ,
,
∴DE、DF、CF的长度之和不变化,ED+DF+FC=2 ![]()
【解析】1)因为抛物线与x轴交于(﹣1,0)(4,0),可以假设y=a(x+1)(x﹣4),由题意a=﹣ ![]() 代入整理即可求出b、c.(2)①利用待定系数法思想求出点C坐标,利用勾股定理的逆定理证明∠ACB=90°,由此即可解决问题;
代入整理即可求出b、c.(2)①利用待定系数法思想求出点C坐标,利用勾股定理的逆定理证明∠ACB=90°,由此即可解决问题;
②根据相似三角形的判定与性质,可得 ![]() =
= ![]() ,
, ![]() =
= ![]() ,根据等式的性质,可得
,根据等式的性质,可得 ![]() +
+ ![]() ,再根据等量代换,可得答案.
,再根据等量代换,可得答案.
【考点精析】通过灵活运用相似三角形的应用,掌握测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,点C在⊙O上,∠CAB的平分线交⊙O于点D,过点D作AC的垂线交AC的延长线于点E,连接BC交AD于点F.
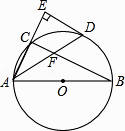
(1)猜想ED与⊙O的位置关系,并证明你的猜想;
(2)若AB=6,AD=5,求AF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】某车间有技术工人85人,平均每天每人可加工甲种部件16个或乙种部件10个,2个甲种部件和3个乙种部件配成一套,问加工甲、乙两种部件各安排多少人才能使每天加工的两种部件刚好配套?并求出加工了多少套?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某次学生夏令营活动,有小学生、初中生、高中生和大学生参加,共200人,各类学生人数比例见扇形统计图.
(1)参加这次夏令营活动的初中生共有多少人?
(2)活动组织者号召参加这次夏令营活动的所有学生为贫困学生捐款结果小学生每人捐款5元,初中生每人捐款10元,高中生每人捐款15元,大学生每人捐款20元问平均每人捐款是多少元?

-
科目: 来源: 题型:
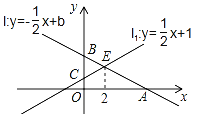
查看答案和解析>>【题目】如图,已知直线l:y=﹣
 x+b与x轴,y轴的交点分别为A,B,直线l1:y=
x+b与x轴,y轴的交点分别为A,B,直线l1:y= x+1与y轴交于点C,直线l与直线ll的交点为E,且点E的横坐标为2.
x+1与y轴交于点C,直线l与直线ll的交点为E,且点E的横坐标为2.(1)求实数b的值和点A的坐标;
(2)设点D(a,0)为x轴上的动点,过点D作x轴的垂线,分别交直线l与直线ll于点M、N,若以点B、O、M、N为顶点的四边形是平行四边形,求a的值.
-
科目: 来源: 题型:
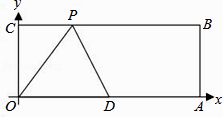
查看答案和解析>>【题目】已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,则P点的坐标为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场用2730元购进A、B两种新型节能日光灯共60盏,这两种日光灯的进价、标价如下表所示.
价格/类型
A型
B型
进价(元/盏)
35
65
标价(元/盏)
50
100
(1)这两种日光灯各购进多少盏?
(2)若A型日光灯按标价的9折出售,要使这批日光灯全部售出后商场获得810元的利润,则B型日光灯应按标价的几折出售?
相关试题

