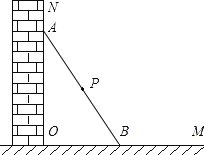
【题目】如图所示,一根长2a的木棍![]() ,斜靠在与地面
,斜靠在与地面![]() 垂直的墙
垂直的墙![]() 上,设木棍的中点为
上,设木棍的中点为![]() 若木棍A端沿墙下滑,且B端沿地面向右滑行.
若木棍A端沿墙下滑,且B端沿地面向右滑行.
![]() 请判断木棍滑动的过程中,点P到点O的距离是否变化,并简述理由.
请判断木棍滑动的过程中,点P到点O的距离是否变化,并简述理由.
![]() 在木棍滑动的过程中,当滑动到什么位置时,
在木棍滑动的过程中,当滑动到什么位置时,![]() 的面积最大?简述理由,并求出面积的最大值.
的面积最大?简述理由,并求出面积的最大值.
参考答案:
【答案】(1)斜边上的中线OP不变;(2)当![]() 的斜边上的高h等于中线OP时,
的斜边上的高h等于中线OP时,![]() 为等腰直角三角形时,面积最大,理由见解析
为等腰直角三角形时,面积最大,理由见解析
【解析】试题分析:(1)木棍滑动的过程中,点P到点O的距离不会变化.根据在直角三角形中,斜边上的中线等于斜边的一半即可判断;
(2)当△AOB的斜边上的高h等于中线OP时,△AOB的面积最大,就可以求出.
试题解析:(1)不变。
理由:在直角三角形中,斜边上的中线等于斜边的一半,因为斜边AB不变,所以斜边上的中线OP不变。
(2)当△AOB的斜边上的高h等于中线OP时,△AOB的面积最大。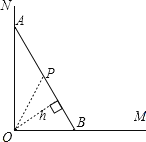
如图,若h与OP不相等,则总有h<OP,
故根据三角形面积公式,有h与OP相等时△AOB的面积最大
此时,S△AOB=![]() AB·h=
AB·h=![]() ×2a·a=a2,所以△AOB的最大面积为a2.
×2a·a=a2,所以△AOB的最大面积为a2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把棱长为1cm的若干个小正方体摆放如图所示的几何体,然后在露出的表面上涂上颜色
 不含底面
不含底面
 该几何体中有多少小正方体?
该几何体中有多少小正方体? 画出主视图.
画出主视图. 求出涂上颜色部分的总面积.
求出涂上颜色部分的总面积.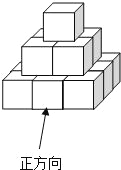
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD是BC边上的高,将△ABD沿AD折叠得到△AED,点E落在CD上,∠B=50°,∠C=30°.
(1)填空:∠BAD= 度;
(2)求∠CAE的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某城市按以下规定收取每月的水费,用水不超过7吨,按每吨1.5元收费;若超过7吨,未超过部分仍按每吨1.5元收取,而超过部分则按每吨2.3元收费.
(1)如果某用户5月份水费平均为每吨1.6元,那么该用户5月份应交水费多少元?
(2)如果某用户5月份交水费17.4元,那么该用户5月份水费平均每吨多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一艘核潜艇在海面DF下600米A点处测得俯角为30°正前方的海底C点处有黑匣子,继续在同一深度直线航行2000米到B点处测得正前方C点处的俯角为45°.求海底C点处距离海面DF的深度(结果保留根号)

-
科目: 来源: 题型:
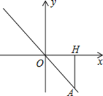
查看答案和解析>>【题目】如图,正比例函数y=kx的图像经过点A,点A在第四象限.过点A做AH⊥x轴,垂足为点H,点A的横坐标为3,且△AOH的面积为4.5.
(1)求该正比例函数的解析式;
(2)在x轴上是否存在一点P,使△AOP的面积为6?若存在,求点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形网格中,每个小正方形的边长为1,网格中有一个格点△ABC(即三角形的顶点都在格点上)
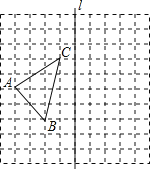
(1)在图中作出△ABC关于直线1对称的△A1B1C1;(要求:A与A1、B与B1、C与C1相对应);
(2)在第(1)问的结果下,连结BB1,CC1,求四边形BB1C1C的面积;
(3)在图中作出△ABC关于点C成中心对称的△A2CB2.
相关试题

