搜索
【题目】如图，在△ABC中，AD是BC边上的高，将△ABD沿AD折叠得到△AED，点E落在CD上，∠B=50°，∠C=30°．
（1）填空：∠BAD= 度；
（2）求∠CAE的度数．
参考答案：
【答案】（1）40；（2）20°
【解析】
（1）直接根据三角形内角和定理求出∠BAD的度数；
（2）先根据图形折叠的性质求出∠AED的度数，再由三角形外角的性质即可得出结论．
（1）∵AD是BC边上的高，∠B=50°，
∴∠BAD=180°-90°-50°=40°．
故答案为：40；
（2）∵△AED是由△ABD折叠得到，
∴∠AED=∠B=50°，
∵∠AED是△ACE的外角，
∴∠AED=∠CAE+∠C，
∴∠CAE=∠AED-∠C=50°-30°=20°．
-
科目： 来源： 题型：
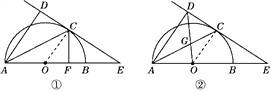
查看答案和解析>>【题目】如图①，AB为半圆的直径，O为圆心，C为圆弧上一点，AD垂直于过C点的切线，垂足为D，AB的延长线交直线CD于点E.
(1)求证：AC平分∠DAB；
(2)若AB＝4，B为OE的中点，CF⊥AB，垂足为点F，求CF的长；
(3)如图②，连接OD交AC于点G，若
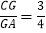，求sinE的值．
【答案】(1)证明见解析；(2)CF＝
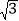；(3) sinE＝
.【解析】分析：（1）连接OC，由平行线的判定定理、性质以及三角形中的等角对等边的原理即可求证。（2）由（1）中结论，利用特殊角的三角函数值可求出∠E=30和CF的长度。（3）连接OC，即可证得△OCG∽△DAG，△OCE∽△DAE，根据相似三角形的对应边成比例，可得EO与AO的比例关系，又因为OC=OA，所以在RT△OCE中由三角函数的定义即可求解。
本题解析：(1)连接OC，如图①.∵OC切半圆O于C，∴OC⊥DC，又AD⊥CD.∴OC∥AD.∴∠OCA＝∠DAC.∵OC＝OA，∴∠OAC＝∠ACO.∴∠DAC＝∠CAO，即AC平分∠DAB.
(2)在Rt△OCE中，∵OC＝OB＝
OE，∴∠E＝30°.∴在Rt△OCF中，CF＝OC·sin60°＝2×
＝
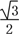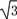.(3)连接OC，如图②.∵CO∥AD，∴△CGO∽△AGD.∴
＝
＝
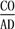.不妨设CO＝AO＝3k，则AD＝4k.又△COE∽△DAE，∴＝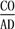
＝＝
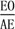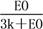.∴EO＝9k.在Rt△COE中，sinE＝
＝
＝
.
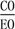【题型】解答题
【结束】
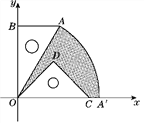
25【题目】如图，有一块含30°角的直角三角板OAB的直角边BO的长恰与另一块等腰直角三角板ODC的斜边OC的长相等，把这两块三角板放置在平面直角坐标系中，且OB＝3
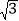.(1)若某反比例函数的图象的一个分支恰好经过点A，求这个反比例函数的解析式；
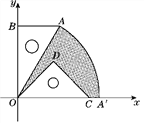
(2)若把含30°角的直角三角板绕点O按顺时针方向旋转后，斜边OA恰好落在x轴上，点A落在点A′处，试求图中阴影部分的面积．(结果保留π)
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，有一块含30°角的直角三角板OAB的直角边BO的长恰与另一块等腰直角三角板ODC的斜边OC的长相等，把这两块三角板放置在平面直角坐标系中，且OB＝3
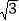.(1)若某反比例函数的图象的一个分支恰好经过点A，求这个反比例函数的解析式；
(2)若把含30°角的直角三角板绕点O按顺时针方向旋转后，斜边OA恰好落在x轴上，点A落在点A′处，试求图中阴影部分的面积．(结果保留π)
【答案】(1)反比例函数的解析式为y＝
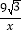；(2)S阴影＝6π－
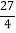.【解析】分析：（1）根据tan30°=
，求出AB，进而求出OA，得出A的坐标，设过A的双曲线的解析式是y=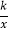
，把A的坐标代入求出即可；（2）求出∠AOA′，根据扇形的面积公式求出扇形AOA′的面积，求出OD、DC长，求出△ODC的面积，相减即可求出答案．本题解析：
(1)在Rt△OBA中，∠AOB＝30°，OB＝3
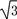，∴AB＝OB·tan 30°＝3.
∴点A的坐标为(3，3
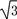)．设反比例函数的解析式为y＝
(k≠0)，∴3
＝
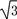，∴k＝9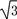，则这个反比例函数的解析式为y＝
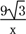.(2)在Rt△OBA中，∠AOB＝30°，AB＝3，
sin ∠AOB＝
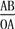，即sin 30°＝
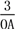，∴OA＝6.
由题意得：∠AOC＝60°，S扇形AOA′＝
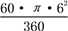＝6π.在Rt△OCD中，∠DOC＝45°，OC＝OB＝3
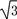，∴OD＝OC·cos 45°＝3
×
＝
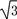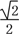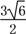.∴S△ODC＝
OD2＝
＝
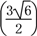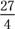.∴S阴影＝S扇形AOA′－S△ODC＝6π－
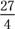.点睛：本题考查了勾股定理、待定系数法求函数解析式、特殊角的三角函数值、扇形的面积及等腰三角形的性质，本题属于中档题，难度不大，将不规则的图形的面积表示成多个规则图形的面积之和是解答本题的关键.
【题型】解答题
【结束】
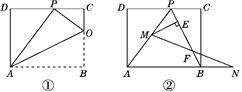
26【题目】矩形ABCD一条边AD＝8，将矩形ABCD折叠，使得点B落在CD边上的点P处．
(1)如图①，已知折痕与边BC交于点O，连接AP，OP，OA.
① 求证：△OCP∽△PDA；
② 若△OCP与△PDA的面积比为1:4，求边AB的长．
(2)如图②，在(1)的条件下，擦去AO和OP，连接BP.动点M在线段AP上(不与点P，A重合)，动点N在线段AB的延长线上，且BN＝PM，连接MN交PB于点F，作ME⊥BP于点E.试问动点M，N在移动的过程中，线段EF的长度是否发生变化？若不变，求出线段EF的长度；若变化，说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】把棱长为1cm的若干个小正方体摆放如图所示的几何体，然后在露出的表面上涂上颜色
不含底面
该几何体中有多少小正方体？
画出主视图．
求出涂上颜色部分的总面积．
-
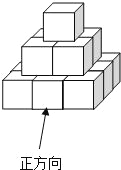
科目： 来源： 题型：
查看答案和解析>>【题目】某城市按以下规定收取每月的水费，用水不超过7吨，按每吨1.5元收费；若超过7吨，未超过部分仍按每吨1.5元收取，而超过部分则按每吨2.3元收费．
（1）如果某用户5月份水费平均为每吨1.6元，那么该用户5月份应交水费多少元？
（2）如果某用户5月份交水费17.4元，那么该用户5月份水费平均每吨多少元？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，一根长2a的木棍
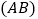，斜靠在与地面
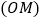垂直的墙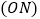
上，设木棍的中点为
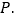若木棍A端沿墙下滑，且B端沿地面向右滑行．
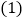请判断木棍滑动的过程中，点P到点O的距离是否变化，并简述理由．
在木棍滑动的过程中，当滑动到什么位置时，
的面积最大？简述理由，并求出面积的最大值．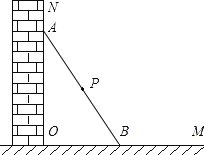
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一艘核潜艇在海面DF下600米A点处测得俯角为30°正前方的海底C点处有黑匣子，继续在同一深度直线航行2000米到B点处测得正前方C点处的俯角为45°．求海底C点处距离海面DF的深度（结果保留根号）
相关试题
