搜索
【题目】如图，在正八边形ABCDEFGH中，四边形BCFG的面积为20cm2 ， 则正八边形的面积为cm2 ．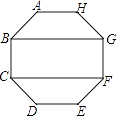 
参考答案：
【答案】40
【解析】解：连接HE，AD， 在正八边形ABCDEFGH中，可得：HE⊥BG于点M，AD⊥BG于点N，
∵正八边形每个内角为： 
=135°，
∴∠HGM=45°，
∴MH=MG，
设MH=MG=x，
则HG=AH=AB=GF= 
x，
∴BG×GF=2（ +1）x2=20，
四边形ABGH面积= 
（AH+BG）×HM=（ +1）x2=10，
∴正八边形的面积为：10×2+20=40（cm2）．
所以答案是：40．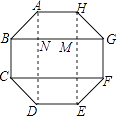
【考点精析】掌握正多边形和圆是解答本题的根本，需要知道圆的内接四边形的对角互补，并且任何一个外角都等于它的内对角；圆的外切四边形的两组对边的和相等．
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读材料
如图①，△ABC与△DEF都是等腰直角三角形，∠ACB=∠EDF=90°，且点D在AB边上，AB、EF的中点均为O，连结BF、CD、CO，显然点C、F、O在同一条直线上，可以证明△BOF≌△COD，则BF=CD．
解决问题
（1）将图①中的Rt△DEF绕点O旋转得到图②，猜想此时线段BF与CD的数量关系，并证明你的结论；
（2）如图③，若△ABC与△DEF都是等边三角形，AB、EF的中点均为O，上述（1）中的结论仍然成立吗？如果成立，请说明理由；如不成立，请求出BF与CD之间的数量关系；
（3）如图④，若△ABC与△DEF都是等腰三角形，AB、EF的中点均为0，且顶角∠ACB=∠EDF=α，请直接写出
的值（用含α的式子表示出来） -
科目： 来源： 题型：
查看答案和解析>>【题目】如图①，若二次函数y=
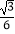x2+bx+c的图象与x轴交于A（﹣2，0），B（3，0）两点，点A关于正比例函数y= 
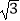x的图象的对称点为C．
（1）求b、c的值；
（2）证明：点C在所求的二次函数的图象上；
（3）如图②，过点B作DB⊥x轴交正比例函数y=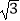 x的图象于点D，连结AC，交正比例函数y= 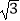x的图象于点E，连结AD、CD．如果动点P从点A沿线段AD方向以每秒2个单位的速度向点D运动，同时动点Q从点D沿线段DC方向以每秒1个单位的速度向点C运动．当其中一个点到达终点时，另一个点随之停止运动，连结PQ、QE、PE．设运动时间为t秒，是否存在某一时刻，使PE平分∠APQ，同时QE平分∠PQC？若存在，求出t的值；若不存在，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】某市在招商引资期间，把已倒闭的机床厂租给外地某投资商，该投资商为减小固定资产投资，将原有的正方形场地改建成800平方米的长方形场地，且其长、宽的比为5：2．
（1）求改建后的长方形场地的长和宽为多少米？
（2）如果把原来面积为900平方米的正方形场地的金属栅栏围墙全部利用，来作为新场地的长方形围墙，栅栏围墙是否够用？为什么？
-
科目： 来源： 题型：
查看答案和解析>>【题目】
（1）计算：|﹣2|﹣
+（﹣2013）0；
（2）计算：（1+
）÷ 
． -
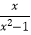科目： 来源： 题型：
查看答案和解析>>【题目】（阅读材料）
∵
＜
＜
，即2＜＜3，∴1＜
＜2．∴
﹣1的整数部分为1．∴
﹣1的小数部分为﹣2（解决问题）9的小数部分是 ；
我们还可以用以下方法求一个无理数的近似值．
阅读理解：求
的近似值．解：设
=10+x，其中0＜x＜1，则107=（10+x）2，即107=100+20x+x2．因为0＜x＜1，所以0＜x2＜1，所以107≈100+20x，解之得x≈0.35，即
的近似值为10.35．理解应用：利用上面的方法求
的近似值（结果精确到0.01）． -
科目： 来源： 题型：
查看答案和解析>>【题目】2012年我国国民经济运行总体平稳，全年全国公共财政收入117210亿元，2008﹣2012年全国公共财政收入及其增长速度情况如图所示：
（1）这五年中全国公共财政收入增长速度最高的年份是年；
（2）2012年的全国公共财政收入比2011年多亿元；
（3）这五年的全国公共财政收入增长速度的平均数是 ．
相关试题
